Тест по теме: Уравнение касательной к графику функции

Пример уравнения касательной

Если дана функция y=f(x) и точка M(a; f(a)) , где существует производная f^{\prime}(a) , мы можем составить уравнение касательной к графику функции в этой точке. Уравнение прямой, не параллельной оси y , всегда имеет вид y=kx+m . Задача сводится к нахождению коэффициентов k и m .

• Угловой коэффициент k определяется производной в точке: k=f^{\prime}(a) .
• Чтобы найти m , используем тот факт, что касательная проходит через точку M(a; f(a)) . Подставляя в уравнение прямой координаты точки M , получаем уравнение f(a)=k \cdot a + m , откуда m=f(a) - k \cdot a .

Теперь подставим найденные значения k и m в уравнение прямой:

y = f(a) + f^{\prime}(a) \cdot (x - a)

Таким образом, мы получили уравнение касательной к графику функции y=f(x) в точке x=a .

Пример 1: Уравнение касательной к графику функции y = x^2 в точке x=1

1. Вычислим f(a)=f(1)=1^2=1 .

2. Производная функции: f^{\prime}(x) = 2x . Тогда f^{\prime}(1) = 2 .

3. Подставим эти значения в уравнение касательной:

y = 1 + 2(x - 1) \quad \Rightarrow \quad y = 2x - 1

Этот результат совпадает с тем, что был получен в предыдущем примере.

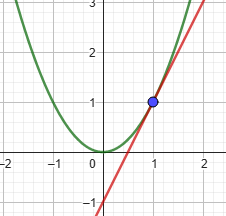
Рисунок 1: График функции y=x^2 с касательной в точке (1, 1).

Пример 2: Касательная к графику функции y = \operatorname{tg}(x) в начале координат

Здесь f(x) = \operatorname{tg}(x) , и касательная проходит через точку a=0 .

1. Вычислим f(0)=\operatorname{tg}(0)=0 .

2. Производная функции: f^{\prime}(x) = \cfrac{1}{\cos^2(x)} . Тогда f^{\prime}(0) = 1 .

3. Подставим в уравнение касательной:

y = 0 + 1(x - 0) \quad \Rightarrow \quad y = x

Таким образом, касательная в начале координат имеет уравнение y = x и составляет угол 45^\circ с осью абсцисс.

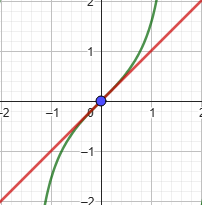
Рисунок 2: График функции y = \operatorname{tg}(x) и касательная y = x .

Алгоритм составления уравнения касательной к графику функции y=f(x)

1. Обозначить абсциссу точки касания буквой a .
2. Вычислить f(a) .
3. Найти f^{\prime}(x) и вычислить f^{\prime}(a) .
4. Подставить найденные значения a , f(a) и f^{\prime}(a) в уравнение касательной.

Пример 3: Уравнение касательной к графику функции y = \cfrac{1}{x} в точке x=1

1. a = 1

2. f(1) = \cfrac{1}{1} = 1

3. Производная функции: f^{\prime}(x) = -\cfrac{1}{x^2} . Тогда f^{\prime}(1) = -1 .

4. Подставим найденные значения в уравнение:

y = 1 - (x - 1) \quad \Rightarrow \quad y = 2 - x

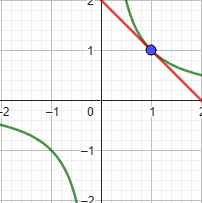
Рисунок 3: График гиперболы y = \cfrac{1}{x} и касательной y = 2 - x .

Пример 4: Найти касательную, параллельную прямой y=4x-5 , к графику y=\cfrac{x^3}{3}

1. Требуется, чтобы угловой коэффициент касательной был равен угловому коэффициенту прямой y=4x-5 , т.е. f^{\prime}(a) = 4 . Производная функции y=\cfrac{x^3}{3} равна f^{\prime}(x) = x^2 . Решая уравнение x^2 = 4 , находим a_1 = 2 и a_2 = -2 .
2. Вычислим значения f(a) :
   • f(2) = \cfrac{2^3}{3} = \cfrac{8}{3}
   • f(-2) = \cfrac{(-2)^3}{3} = -\cfrac{8}{3}
3. Подставляем в уравнение касательной:
   • Для a_1 = 2 : y = \cfrac{8}{3} + 4(x - 2) \quad \Rightarrow \quad y = 4x - \cfrac{16}{3}
   • Для a_2 = -2 : y = -\cfrac{8}{3} + 4(x + 2) \quad \Rightarrow \quad y = 4x + \cfrac{16}{3}

Приближенные вычисления через касательные

Для функции y=f(x) приближенное значение функции в точке x можно выразить через производную:

f(x) \approx f(a) + f^{\prime}(a)(x - a)

Например, для нахождения 1.02^7 используем функцию f(x) = x^7 и производную f^{\prime}(x) = 7x^6 .

1. При a=1 , f(1)=1 , f^{\prime}(1)=7 . Подставляем в уравнение:

1.02^7 \approx 1 + 7 \cdot 0.02 = 1.14

Реальное значение 1.02^7 на калькуляторе: 1.1487 . Разница минимальна, приближение вполне точное.

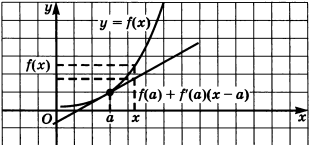
Рисунок 5: Графическое представление приближенного значения 1.02^7 .

Таким образом, использование касательных позволяет не только находить уравнения для различных функций, но и приближенно вычислять значения сложных выражений.

Найти уравнение касательной к функции

f(x) = x^{2} в точке x=0

f(a)=f(1)=1^{2}=1

f'(x)=2x

f'(a)=f'(1)=2\cdot1=2

Вставим данные в формулу

y=f(a)+f^{\prime}(a)(x-a)

y=1+2(x-1)\\{}\\ y=2x-1

Найти уравнение касательной к функции

y=\operatorname{tg} x

в точке x=0

f(a)=\operatorname{tg} 0 = 0

f'(x)={\cfrac{1}{\cos^{2}x}}\\{}\\ f'(a)=f'(0)=1

Вставим данные в формулу

y=f(a)+f^{\prime}(a)(x-a)

y=0+1\cdot(x-0)\\{}\\ y=x

Найти приближенное значение числового выра­жения 1,02^7

f(x)=x^7

f'(x)=7x^6

a=1

x=1.02

f(a)=f(1)=1

f'(a)=f'(1)=7\cdot1^{6}=7

Вставим данные в формулу

y\approx f(a)+f^{\prime}(a)(x-a)\\{}\\ 1,02^7 \approx 1 + 7(1.02-1)=1.14

Выяснить, чему равен угловой коэффициент касательной к параболе y=1-x^2 в точке:
A(0 ; 1)

y^{\prime}(x)=(1)^{\prime}-\Big(x^2\Big)^{\prime}=

0-2 x=-2 x

k=y^{\prime}(0)=-2 \cdot 0=0

Выяснить, чему равен угловой коэффициент касательной к параболе y=1- x^2 в точке:
B(2 ;-3)

y^{\prime}(x)=(1)^{\prime}-\Big(x^2\Big)^{\prime}=

0-2 x=-2 x

k=y^{\prime}(2)=-2 \cdot 2=-4

Выяснить, чему равен угловой коэффициент касательной к параболе y=1- x^2 в точке:
C\Big(\cfrac{1}{2} ; \cfrac{3}{4}\Big)

y^{\prime}(x)=(1)^{\prime}-\Big(x^2\Big)^{\prime}=

0-2 x=-2 x \\ k=y^{\prime}\Big(\cfrac{1}{2}\Big)=

-2 \cdot \cfrac{1}{2}=-1

Выяснить, чему равен угловой коэффициент касательной к параболе y=1- x^2 в точке:
D(-1,03)

y^{\prime}(x)=(1)^{\prime}-\Big(x^2\Big)^{\prime}=

0-2 x=-2 x

k=y^{\prime}(-1)=-2 \cdot(-1)=2

Определить, какой угол образует с осью x касательная, проведенная к графику функции y=f(x) в точке с абсциссой x=a , если: f(x)=x^2, a=0,5 ;

f^{\prime}(x)=\Big(x^2\Big)^{\prime}=2 x

\operatorname{tg} a=f^{\prime}(0,5)=2 \cdot 0,5=1 ;

a=\operatorname{arctg} 1=45^{\circ}

Определить, какой угол образует с осью x касательная, проведенная к графику функции y=f(x) в точке с абсциссой x=a , если: f(x)=-3 x^3, a=\cfrac{1}{3} ;

f^{\prime}(x)=-3\Big(x^3\Big)^{\prime}=-3 \cdot 3 x^2=-9 x^2 ;

\operatorname{tg} a=f^{\prime}\Big(\cfrac{1}{3}\Big)=-9 \cdot\Big(\cfrac{1}{3}\Big)^2=-9 \cdot \cfrac{1}{9}=-1 ;

a=180^{\circ}-\operatorname{arctg} 1=180^{\circ}-45^{\circ}=135^{\circ} ;

Определить, какой угол образует с осью x касательная, проведенная к графику функции y=f(x) в точке с абсциссой x=a , если: f(x)=0,2 x^5, a=-1 ;

f^{\prime}(x)=0,2\Big(x^5\Big)^{\prime}=0,2 \cdot 5 x^4=x^4 ;

\operatorname{tg} a=f^{\prime}(-1)=(-1)^4=1 ;

a=\operatorname{arctg} 1=45^{\circ} ;

Определить, какой угол образует с осью x касательная, проведенная к графику функции y=f(x) в точке с абсциссой x=a , если: f(x)=-0,25 x^4, a=0 ;

f^{\prime}(x)=-0,25\Big(x^4\Big)^{\prime}=-0,25 \cdot 4 x^3=-x^3 \text {; }

\operatorname{tg} a=f^{\prime}(0)=-0^3=0 ;

a=\operatorname{arctg} 0=0^{\circ} ;

f(x)=x^2, a=3 ; Значение функции:

f(a)=3^2=9 \text {; }

Значение производной:

f^{\prime}(x)=\Big(x^2\Big)^{\prime}=2 x ;

f^{\prime}(a)=2 \cdot 3=6 ;

Уравнение касательной:

y=f(a)+f^{\prime}(a)(x-a) ;

y=9+6(x-3)=

9+6 x-18=6 x-9 ;

Ответ: y=6 x-9 .

f(x)=2-x-x^3, a=0 ;

Значение функции:

f(a)=2-0-0^3=2 \text {; }

Значение производной:

f^{\prime}(x)=(2-x)^{\prime}-\Big(x^3\Big)^{\prime}=

-1-3 x^2 ;

f^{\prime}(a)=-1-3 \cdot 0^2=-1 ;

уравнение касательной:

y=f(a)+f^{\prime}(a)(x-a) ;

y=2-1 \cdot(x-0)=2-x

Ответ: y=2-x .

f(x)=x^3, a=1

Значение функции:

f(\text { a })=1^3=1 \text {; }

Значение производной:

f^{\prime}(x)=\Big(x^3\Big)^{\prime}=3 x^2 ;

f^{\prime}(a)=3 \cdot 1^2=3 ;

Уравнение касательной:

y=f(a)+f^{\prime}(a)(x-a) ;

y=1+3(x-1)=

1+3 x-3=3 x-2 ;

Ответ: y=3 x-2 .

f(x)=x^3-3 x+5, \quad a=-1 ;

Значение функции:

f(a)=(-1)^3-3 \cdot(-1)+5=-1+3+5=7 ;

Значение производной:

f^{\prime}(x)=\Big(x^3\Big)^{\prime}+(-3 x+5)^{\prime}=3 x^2-3 ;

f^{\prime}(a)=3 \cdot(-1)^2-3=3-3=0 ;

Уравнение касательной:

y=f(a)+f^{\prime}(a)(x-a) ;

y=7+0 \cdot(x-(-1))=7 ;

Ответ: y=7 .