Тригонометрические функции
Тригонометрические функции
Свойства тригонометрических функций
Основные тригонометрические тождества
Формулы приведения
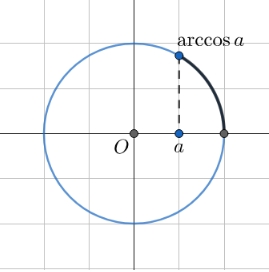
Арккосинус
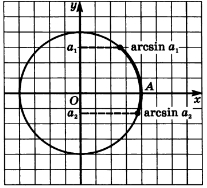
Арксинус
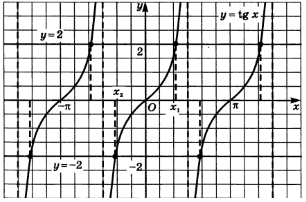
Арктангенс
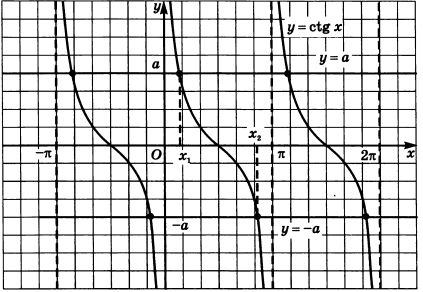
Арккотангенс
Простейшие тригонометрические уравнения
Методы решения тригонометрических уравнений
Однородные тригонометрические уравнения первой степени
Однородные тригонометрические уравнения второй степени
Синус и косинус суммы и разности аргументов
Тангенс суммы и разности аргументов
Формулы двойного аргумента
Производная
Предел функции на бесконечности
Предел функции в точке
Приращение функции
Производная
Формулы дифференцирования
Правила дифференцирования
Уравнение касательной к графику функции
Исследование функций на монотонность
Точки экстремума функции
Нахождение наибольшего и наименьшего значений
Тест по теме: Тангенс суммы и разности аргументов
Теория:
Тестовые вопросы и практика:
Тангенс суммы
Тангенс разности
Пример
Найдите значение
Упростите
x}{1+{\mathrm{tg}}\cfrac{\pi}{4}{\mathrm{tg}}x}=