Арктангенс и решение уравнения tg x = a

Введение

Арктангенс является важной функцией в тригонометрии и находит широкое применение в математике, физике, инженерии и многих других областях. Это обратная функция для тангенса, которая позволяет вычислить угол по известному значению тангенса. Решение уравнения \text{tg } x = a напрямую связано с арктангенсом, и в этой статье мы подробно разберём эти понятия, а также методы решения уравнения.

Арктангенс: определение и свойства

Арктангенс, обозначаемый как \text{arctg } x или \text{tg }^{-1} x , является обратной функцией для тангенса, т.е. если y = \text{tg } x , то x = \text{arctg } y .

Арктангенс определён для всех вещественных чисел y \in (-\infty, +\infty) , и его область значений (значения углов) лежит в интервале:

\text{arctg } y \in \Big(-\cfrac{\pi}{2}, \cfrac{\pi}{2}\Big)

Это связано с тем, что функция \text{tg } x на интервале \Big(-\cfrac{\pi}{2}, \cfrac{\pi}{2}\Big) является строго возрастающей и принимает все значения от -\infty до +\infty .

Свойства функции арктангенс:

1. Область определения: x \in (-\infty, +\infty) .
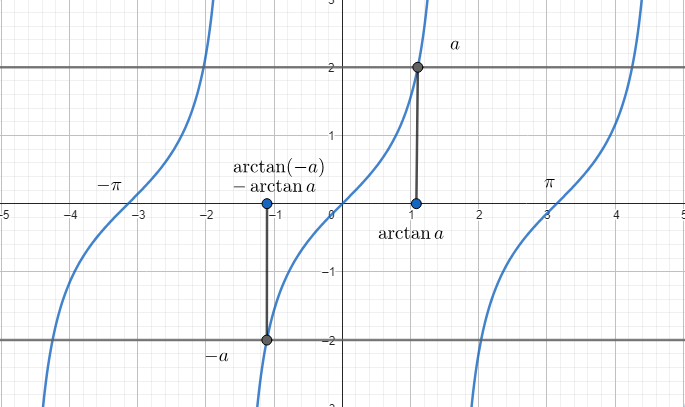
2. Область значений: \text{arctg } x \in \Big(-\cfrac{\pi}{2}, \cfrac{\pi}{2}\Big) .
3. Чётность: \text{arctg }(-x) = -\text{arctg }(x) (нечётная функция).
4. Пределы:
   • \lim\_{x \to +\infty} \text{arctg } x = \cfrac{\pi}{2} ,
   • \lim\_{x \to -\infty} \text{arctg } x = -\cfrac{\pi}{2} .

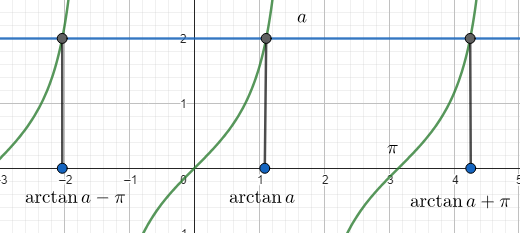
Решение уравнения \text{tg } x = a

Рассмотрим уравнение вида:

\text{tg } x = a,

где a — некоторое известное число. Для того чтобы решить это уравнение, мы можем использовать функцию арктангенс. В первую очередь нужно найти основной корень уравнения:

x\_0 = \text{arctg } a.

Поскольку тангенс — периодическая функция с периодом \pi , общее решение уравнения будет:

x = \text{arctg } a + n\pi, \quad n \in \mathbb{Z}.

Пример 1: Решение уравнения \text{tg } x = 1

Найдем решение уравнения \text{tg } x = 1 . Известно, что:

\text{arctg } 1 = \cfrac{\pi}{4}.

Следовательно, общее решение:

x = \cfrac{\pi}{4} + n\pi, \quad n \in \mathbb{Z}.

Пример 2: Решение уравнения \text{tg } x = -\sqrt{3}

Для уравнения \text{tg } x = -\sqrt{3} находим основной корень:

\text{arctg }(-\sqrt{3}) = -\cfrac{\pi}{3}.

Общее решение:

x = -\cfrac{\pi}{3} + n\pi, \quad n \in \mathbb{Z}.

Решение уравнения в заданном интервале

Иногда уравнение нужно решить на определённом интервале, например, x \in [0, 2\pi] . В таких случаях необходимо подставить разные значения n в общее решение и выбрать те значения x , которые лежат в нужном интервале.

Пример 3: Решение уравнения \text{tg } x = 2 на интервале [0, 2\pi]

1. Находим основной корень:

x\_0 = \text{arctg } 2 \approx 1.107.

2. Общее решение:

x = 1.107 + n\pi.

3. Теперь проверим, какие значения x попадают в интервал [0, 2\pi] .

• При n = 0 , x\_0 \approx 1.107 \in [0, 2\pi] .
• При n = 1 , x\_1 = 1.107 + \pi \approx 4.249 \in [0, 2\pi] .
• При n = 2 , x\_2 = 1.107 + 2\pi \approx 7.391 \notin [0, 2\pi] .

Таким образом, решение на интервале [0, 2\pi] будет:

x \approx 1.107 \text{и} x \approx 4.249.

Арктангенс является обратной функцией тангенса и играет важную роль в решении тригонометрических уравнений вида \text{tg } x = a . Для нахождения решения такого уравнения используется основной корень x\_0 = \text{arctg } a , а затем общее решение записывается с учётом периодичности функции тангенс. Важно также учитывать дополнительные условия, например, решение на заданном интервале.

уравнение \text{tg} x= a имеет решение x=\text{arctg} a+\pi k, k \in Z

Вообще для любого значения a справедлива формула \text{arctg}(-a)=-\text{arctg} a

Найти \operatorname{arctg}\Big(-\cfrac{1}{\sqrt{3}}\Big)
\text{arctg}\Big(-\cfrac{1}{\sqrt{3}}\Big)=

-\text{arctg}\cfrac{1}{\sqrt{3}}= -\cfrac{\pi}{6}
2{n} 3{n} 4{n}

\text{arcctg}\Big(-\cfrac{\sqrt{3}}{3}\Big)-\text{arctg} \cfrac{\sqrt{3}}{3}=

\pi-\text{arcctg} \cfrac{\sqrt{3}}{3}-\text{arctg} \cfrac{\sqrt{3}}{3}=

\pi-\cfrac{\pi}{3}-\cfrac{\pi}{6}=

\cfrac{6 \pi}{6}-\cfrac{2 \pi}{6}-\cfrac{\pi}{6}=

\cfrac{3 \pi}{6}=\cfrac{\pi}{2} ;

\operatorname{arccos}\Big(-\cfrac{1}{2}\Big)-\operatorname{arcctg}(-\sqrt{3})=

\pi-\arccos \cfrac{1}{2}-(\pi-\operatorname{arcctg} \sqrt{3})=\\

\pi-\cfrac{\pi}{3}-\pi+\cfrac{\pi}{6}=

-\cfrac{2 \pi}{6}+\cfrac{\pi}{6}=-\cfrac{\pi}{6} ;