Тест по теме: Предел функции в точке

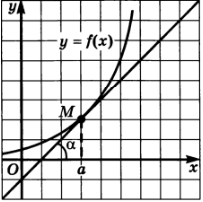
Предел функции в точке

Понятие предела функции в точке является одним из ключевых понятий в математическом анализе, лежащим в основе многих других концепций, таких как непрерывность и дифференцируемость. Рассмотрим несколько примеров, чтобы понять, как вычисляется предел функции в точке и какие существуют особенности.

Графическая иллюстрация предела функции

Рассмотрим три графика функций, изображенные на рисунках 122-124. Визуально может показаться, что это одна и та же кривая, однако функции различаются своим поведением в точке x = a . Проанализируем каждую ситуацию:

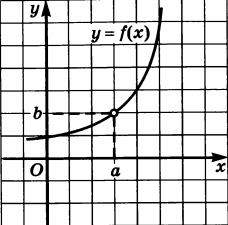
1. Функция на рисунке 122: В точке x = a функция не определена, значение f(a) не существует. Предел функции может существовать, несмотря на отсутствие значения в данной точке.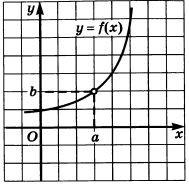

   

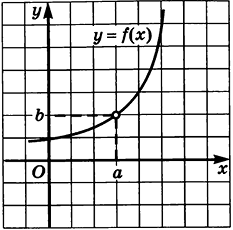
2. Функция на рисунке 123: В точке x = a значение f(a) существует, но оно не совпадает с тем значением, к которому стремятся значения функции при приближении аргумента x к a .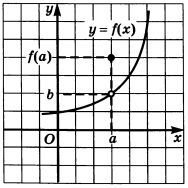

   

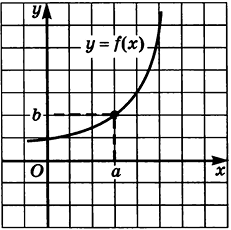
3. Функция на рисунке 124: В этой ситуации значение f(a) существует и равно предельному значению функции при x \to a , то есть f(a) = b .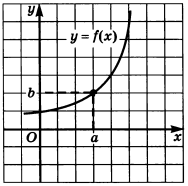

   

Во всех трех случаях используется одинаковая запись:

\lim\limits_{x \to a} f(x) = b

Этот символ означает, что если значения аргумента x всё ближе и ближе приближаются к a , то значения функции f(x) приближаются к числу b . Важно подчеркнуть, что сама точка x = a может не входить в область определения функции — для вычисления предела достаточно только поведения функции вблизи этой точки.

Непрерывность функции

Как видно из примеров, можно задаться вопросом: какая из представленных функций является непрерывной в точке x = a ? Ответ очевиден — третья функция (рис. 124). Для неё справедливо соотношение:

\lim\limits_{x \to a} f(x) = f(a)

Это условие называется непрерывностью функции в точке. В более общем смысле, функция непрерывна на некотором промежутке, если она непрерывна в каждой точке этого промежутка.

Определение 1. Непрерывность функции в точке

Функция y = f(x) называется непрерывной в точке x = a , если выполняется следующее условие:

\lim\limits_{x \to a} f(x) = f(a)

Другими словами, функция непрерывна в точке x = a , если предел функции при стремлении x к a равен значению функции в этой точке.

Примеры вычисления предела функции

Пример 3. Вычисление предела полинома

Найдем предел функции:

\lim\limits_{x \to 1} \Big( x^3 - 2x^2 + 5x + 3 \Big)

Так как выражение x^3 - 2x^2 + 5x + 3 определено во всех точках, в том числе и в точке x = 1 , то функция является непрерывной в этой точке. Следовательно, предел функции равен её значению при x = 1 :

\lim\limits_{x \to 1} \Big( x^3 - 2x^2 + 5x + 3 \Big) = 1^3 - 2 \cdot 1^2 + 5 \cdot 1 + 3 = 7

Пример 4. Предел тригонометрической функции

Найдем предел функции:

\lim\limits_{x \to 2} \cfrac{\sin (\pi x)}{\sqrt{x} + 4}

Функция \cfrac{\sin (\pi x)}{\sqrt{x} + 4} определена на промежутке [0; +\infty) и непрерывна в точке x = 2 . Следовательно, предел функции равен её значению в точке x = 2 :

\lim\limits_{x \to 2} \cfrac{\sin (\pi x)}{\sqrt{x} + 4} = \cfrac{\sin 2\pi}{\sqrt{2} + 4} = \cfrac{0}{\sqrt{2} + 4} = 0

Пример 5. Предел дробно-рациональной функции

Найдем предел:

\lim\limits_{x \to -3} \cfrac{x^2 - 9}{4x + 12}

Если подставить x = -3 , то мы получим неопределенность вида \cfrac{0}{0} . Чтобы избавиться от этой неопределенности, разложим числитель на множители:

\cfrac{x^2 - 9}{4x + 12} = \cfrac{(x - 3)(x + 3)}{4(x + 3)} = \cfrac{x - 3}{4}, \quad x \neq -3

Теперь можем вычислить предел:

\lim\limits_{x \to -3} \cfrac{x - 3}{4} = \cfrac{-3 - 3}{4} = -\cfrac{6}{4} = -1.5

Таким образом, предел функции в точке x = -3 равен -1.5 .

Теорема об арифметических операциях над пределами

Существует важная теорема, которая облегчает вычисление пределов функций, позволяя оперировать с их значениями по аналогии с числами. Пусть \lim\limits_{x \to \alpha} f(x) = b , \lim\limits_{x \to \alpha} g(x) = c . Тогда:

1. \lim\limits_{x \to \alpha} (f(x) + g(x)) = b + c — предел суммы равен сумме пределов.
2. \lim\limits_{x \to \alpha} (f(x) g(x)) = bc — предел произведения равен произведению пределов.
3. \lim\limits_{x \to \alpha} \cfrac{f(x)}{g(x)} = \cfrac{b}{c} , если c \neq 0 — предел частного равен частному пределов.
4. \lim\limits_{x \to \alpha} k f(x) = k \cdot b , где k — константа.

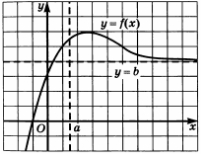
Пример 6. Построение графика функции с заданными условиями

Построим график функции y = f(x) , которая обладает следующими свойствами:

1. Область определения: D(f) = (-\infty; +\infty)
2. \lim\limits_{x \to -2} f(x) = 0
3. f(-2) = 1 , f(0) = 4
4. \lim\limits_{x \to +\infty} f(x) = 0
5. f(x) \lt 0 при x \lt -2

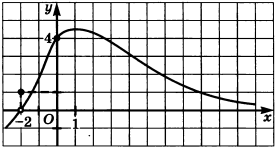
График может выглядеть так, как представлено на рисунке 125.

Заключение

Предел функции в точке — это фундаментальное понятие анализа, которое помогает описать поведение функции вблизи точки. Понятие предела тесно связано с непрерывностью, что позволяет классифицировать функции и их поведение в зависимости от того, как они себя ведут при приближении аргумента к заданной точке.