Тригонометрические функции
Тригонометрические функции
Свойства тригонометрических функций
Основные тригонометрические тождества
Формулы приведения
Арккосинус
Арксинус
Арктангенс
Арккотангенс
Простейшие тригонометрические уравнения
Методы решения тригонометрических уравнений
Однородные тригонометрические уравнения первой степени
Однородные тригонометрические уравнения второй степени
Синус и косинус суммы и разности аргументов
Тангенс суммы и разности аргументов
Формулы двойного аргумента
Производная
Предел функции на бесконечности
Предел функции в точке
Приращение функции
Производная
Формулы дифференцирования
Правила дифференцирования
Уравнение касательной к графику функции
Исследование функций на монотонность
Точки экстремума функции
Нахождение наибольшего и наименьшего значений
Тест по теме: Функция корня n-ной степени
Теория:
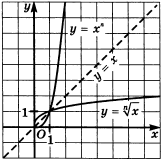
Функция обратная степенной

Функция y=x^n , x \in [0;+\infty) монотонна, значит, обратима.
.
y={\sqrt[n ]{x}} является обратной для функции y=x^{n } , а потому график функции
y = {\sqrt[n]{x}}, x \gt 0 симметричен графику функции y =x^n, xgeqslant0 относительно
прямой y = x
- Выразив
x черезy из уравненияy=x^n , получим:x={\sqrt[ n]{y}} . - Поменяв
x иy местами, получимy={\sqrt[n ]{x}} .
Свойства функции
D(f)= [0;+\infty) - функция не является ни четной, ни нечетной;
- возрастает на
[0;+\infty) - не ограничена сверху, ограничена снизу
- не имеет наибольшего значения,
y_{наим}=0 - непрерывна
E(f)= [0;+\infty)
Дифференцируемость
точке, ее производная равна n x^{n-1} касательную. Этим же свойством обладает и
график функции y={\sqrt[n]{x}} : в любой его точке к графику можно
провести касательную. Таким образом, мы можем отметить еще одно
свойство функции y={\sqrt[n]{x}} :
Пример
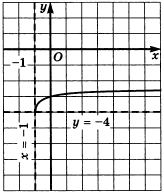
Построить график функции
- Перейдем к
вспомогательной системе координат с началом
в точке
(-1;-4) — пунктирные прямыеx= -1 иy = -4 проведены на рисунке - «Привяжем» функцию
y={sqrt{x}} к новой системе координат. Это и будет требуемый график.