Тест по теме: Приращение функции

Приращение аргумента и приращение функции

Изучение изменения функции вблизи конкретной точки играет важную роль в математическом анализе. Чтобы формализовать это изменение, используют понятия приращения аргумента и приращения функции.

Определение приращения аргумента и функции

Определение: Пусть функция y = f(x) определена в двух точках x_0 и x_1 . Тогда:

• Приращением аргумента при переходе от x_0 к x_1 называют разность \Delta x = x_1 - x_0 .
• Приращением функции при этом переходе называют разность \Delta y = f(x_1) - f(x_0) , также обозначаемую как \Delta f .

Таким образом, можно записать:
\Delta y = f(x_0 + \Delta x) - f(x_0).
Это выражение показывает, как изменяется значение функции при изменении аргумента на \Delta x .

Пример 1. Приращение функции y = x^2

Задача: Найти приращение функции y = x^2 при переходе от точки x_0 = 1 к:

• x_1 = 1.1 ;
• x_1 = 0.98 .

Решение:

1. Функция задана как f(x) = x^2 .

   а) Для x_1 = 1.1 :
   f(1) = 1^2 = 1, \quad f(1.1) = 1.1^2 = 1.21.
   Тогда приращение функции:
   \Delta y = f(1.1) - f(1) = 1.21 - 1 = 0.21.

   б) Для x_1 = 0.98 :
   f(1) = 1^2 = 1, \quad f(0.98) = 0.98^2 = 0.9604.
   Тогда приращение функции:
   \Delta y = f(0.98) - f(1) = 0.9604 - 1 = -0.0396.

Как видим, приращение функции может быть как положительным, так и отрицательным, что зависит от направления изменения аргумента.

---

Непрерывность функции через приращения

Теперь посмотрим, как можно определить непрерывность функции через приращения аргумента и функции.

Определение: Функция y = f(x) непрерывна в точке x = a , если при \Delta x \to 0 (то есть, при приближении x к a ) также выполняется \Delta y \to 0 , то есть приращение функции стремится к нулю.

Таким образом, условие непрерывности можно переформулировать так:
\text{если} , \Delta x \to 0, , \text{то} , \Delta y \to 0.

Для функций, заданных на отрезке, непрерывность в крайних точках понимается следующим образом:

• В левой конечной точке a при \Delta x gt; 0 , если \Delta x \to 0 , то \Delta y \to 0 .
• В правой конечной точке b при \Delta x lt; 0 , если \Delta x \to 0 , то \Delta y \to 0 .

Например, функция y = \sqrt{x} непрерывна на луче [0; +\infty) , включая точку x = 0 .

---

Примеры вычисления приращений функции

Пример 2. Линейная функция

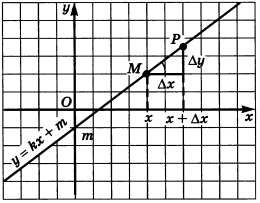
Задача: Для функции y = kx + m найти:

1. Приращение функции при переходе от точки x к точке x + \Delta x ;
2. Предел отношения приращения функции к приращению аргумента при \Delta x \to 0 .

Решение:

1. Приращение функции:
   f(x + \Delta x) = k(x + \Delta x) + m = kx + k\Delta x + m.
   Тогда приращение функции:
   \Delta y = f(x + \Delta x) - f(x) = (kx + k\Delta x + m) - (kx + m) = k\Delta x.

2. Предел отношения приращений:
   \lim \limits_{\Delta x \to 0} \cfrac{\Delta y}{\Delta x} = \lim \limits_{\Delta x \to 0} \cfrac{k \Delta x}{\Delta x} = k.

Таким образом, приращение функции пропорционально приращению аргумента, а отношение приращений всегда равно угловому коэффициенту k .

---

Пример 3. Квадратичная функция

Задача: Для функции y = x^2 найти:

1. Приращение функции при переходе от точки x к точке x + \Delta x ;
2. Предел отношения приращения функции к приращению аргумента при \Delta x \to 0 .

Решение:

1. Приращение функции:
   f(x + \Delta x) = (x + \Delta x)^2 = x^2 + 2x\Delta x + (\Delta x)^2.
   Тогда приращение функции:
   \Delta y = f(x + \Delta x) - f(x) = (x^2 + 2x\Delta x + (\Delta x)^2) - x^2 = 2x\Delta x + (\Delta x)^2.

2. Предел отношения приращений:
   \lim \limits_{\Delta x \to 0} \cfrac{\Delta y}{\Delta x} = \lim \limits_{\Delta x \to 0} \cfrac{2x\Delta x + (\Delta x)^2}{\Delta x} = \lim \limits_{\Delta x \to 0}(2x + \Delta x) = 2x.

Таким образом, приращение функции y = x^2 не пропорционально приращению аргумента, а предел отношения приращения функции к приращению аргумента равен 2x , что является производной функции y = x^2 в точке x .

---

Заключение

Понятие приращений аргумента и функции важно для понимания изменения функций, их непрерывности и поведения в различных точках. Эти понятия также служат основой для дифференциального исчисления и анализа производных.