Свойства тригонометрических функций
Тригонометрические функции — синус, косинус, тангенс и котангенс — обладают рядом симметричных свойств, которые помогают более эффективно решать задачи, связанные с углами, периодичностью и симметрией. Рассмотрим четыре важных свойства этих функций, докажем их и приведем примеры.
Свойство 1: Симметрия функций при отрицательных углах
Для любого значения t справедливы следующие равенства:
\sin (-t)=-\sin t, \quad \cos (-t)=\cos t,
\operatorname{tg}(-t)=-\operatorname{tg} t, \quad \operatorname{ctg}(-t)=-\operatorname{ctg} t.
Пример:
\sin \Big(-\cfrac{\pi}{6}\Big) = -\sin \cfrac{\pi}{6} = -\cfrac{1}{2},
\cos \Big(-\cfrac{\pi}{4}\Big) = \cos \cfrac{\pi}{4} = \cfrac{\sqrt{2}}{2}.
Доказательство:
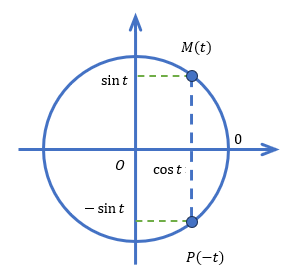
Пусть точке t на числовой окружности соответствует точка M , а точке -t — точка P , симметричная M относительно горизонтальной оси (оси абсцисс). У таких точек совпадают абсциссы (поэтому \cos(-t) = \cos t ), но ординаты противоположны по знаку ( \sin(-t) = -\sin t ).
Для тангенса и котангенса используем определения:
\operatorname{tg}(-t) = \cfrac{\sin(-t)}{\cos(-t)} = \cfrac{-\sin t}{\cos t} = -\operatorname{tg} t,
\operatorname{ctg}(-t) = \cfrac{\cos(-t)}{\sin(-t)} = \cfrac{\cos t}{-\sin t} = -\operatorname{ctg} t.
Свойство 2: Периодичность синуса и косинуса
Для любого значения t выполняются равенства:
\sin(t + 2 \pi k) = \sin t, \quad \cos(t + 2 \pi k) = \cos t.
Здесь k — любое целое число.
Доказательство:
Числа t и t + 2 \pi k соответствуют одной и той же точке на числовой окружности, так как окружность замыкается каждые 2 \pi . Следовательно, значения синуса и косинуса для углов, отличающихся на полный оборот (или его кратные), совпадают.
Свойство 3: Смещение на \pi
Для любого значения t справедливы следующие равенства:
\sin(t + \pi) = -\sin t, \quad \cos(t + \pi) = -\cos t,
\operatorname{tg}(t + \pi) = \operatorname{tg} t, \quad \operatorname{ctg}(t + \pi) = \operatorname{ctg} t.
Пример:
\sin \cfrac{7 \pi}{6} = \sin \Big(\cfrac{\pi}{6} + \pi\Big) = -\sin \cfrac{\pi}{6} = -\cfrac{1}{2},
\cos \cfrac{5 \pi}{4} = \cos \Big(\cfrac{\pi}{4} + \pi\Big) = -\cos \cfrac{\pi}{4} = -\cfrac{\sqrt{2}}{2}.
Доказательство:
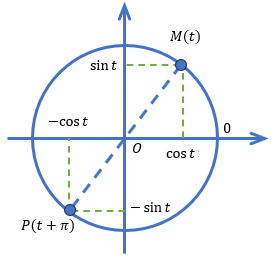
Числу t на числовой окружности соответствует точка M , а числу t + \pi — точка P , симметричная M относительно центра окружности. У таких точек абсциссы и ординаты одинаковы по модулю, но противоположны по знаку. Поэтому:
\cos(t + \pi) = -\cos t, \quad \sin(t + \pi) = -\sin t.
Для тангенса и котангенса:
\operatorname{tg}(t + \pi) = \cfrac{\sin(t + \pi)}{\cos(t + \pi)} = \cfrac{-\sin t}{-\cos t} = \operatorname{tg} t,
\operatorname{ctg}(t + \pi) = \cfrac{\cos(t + \pi)}{\sin(t + \pi)} = \cfrac{-\cos t}{-\sin t} = \operatorname{ctg} t.
Свойство 4: Смещение на \cfrac{\pi}{2}
Для любого значения t выполняются равенства:
\sin \Big(t + \cfrac{\pi}{2}\Big) = \cos t, \quad \cos \Big(t + \cfrac{\pi}{2}\Big) = -\sin t.
Доказательство:
Пусть точке t на числовой окружности соответствует точка M , а точке t + \cfrac{\pi}{2} — точка P , которая на четверть оборота смещена относительно M . Дуги, соответствующие этим точкам, равны, и их проекции на оси можно сравнить через равенство прямоугольных треугольников на окружности.
Таким образом, ордината точки P совпадает с абсциссой точки M , а абсцисса P равна ординате M , но с противоположным знаком. Следовательно:
\sin \Big(t + \cfrac{\pi}{2}\Big) = \cos t, \quad \cos \Big(t + \cfrac{\pi}{2}\Big) = -\sin t.
Примеры и задачи
Пример Доказать тождества:
a) \sin(\pi - t) = \sin t ,
б) \cos(\pi - t) = -\cos t ,
в) \sin(2\pi - t) = -\sin t ,
г) \cos(2\pi - t) = \cos t .
Решение.
а) Запишем \sin(\pi - t) как \sin(-t + \pi) . Применив свойство 3:
\sin(-t + \pi) = -\sin(-t).
По свойству 1, \sin(-t) = -\sin t , тогда:
-\sin(-t) = \sin t.
б) Запишем \cos(\pi - t) как \cos(-t + \pi) . Применив свойство 3:
\cos(-t + \pi) = -\cos(-t),
по свойству 1, \cos(-t) = \cos t , значит:
\cos(\pi - t) = -\cos t.
в) \sin(2\pi - t) = \sin(-t + 2\pi) = \sin(-t) = -\sin t .
г) \cos(2\pi - t) = \cos(-t + 2\pi) = \cos(-t) = \cos t .
Пример 9. Вычислить: а) \operatorname{tg}\Big(-\cfrac{7\pi}{3}\Big) , б) \operatorname{ctg}\Big(\cfrac{5\pi}{4}\Big) .
Решение.
а) По свойству 1:
\operatorname{tg}\Big(-\cfrac{7\pi}{3}\Big) = -\operatorname{tg} \cfrac{7\pi}{3}.
Так как \cfrac{7\pi}{3} = 2\pi + \cfrac{\pi}{3} , то:
-\operatorname{tg} \cfrac{7\pi}{3} = -\operatorname{tg} \cfrac{\pi}{3} = -\sqrt{3}.
б) \operatorname{ctg} \cfrac{5\pi}{4} = \operatorname{ctg}\Big(\pi + \cfrac{\pi}{4}\Big) = \operatorname{ctg} \cfrac{\pi}{4} = 1 .
Эти свойства позволяют легко решать задачи с углами и анализировать поведение тригонометрических функций.