Применение производной для исследования функций на монотонность и экстремумы

1\. Исследование функций на монотонность

Производная функции – это мощный инструмент для исследования ее монотонности и нахождения экстремумов. Рассмотрим, как анализ производной помогает определить, на каких интервалах функция возрастает или убывает, а также, где она имеет экстремумы.

Возрастание функции

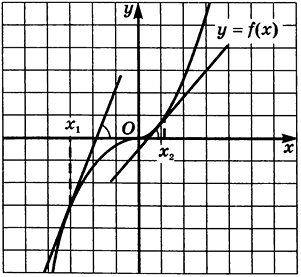
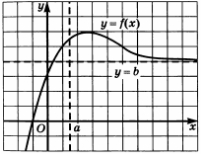
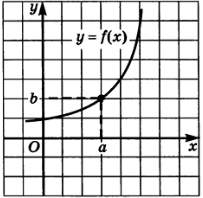
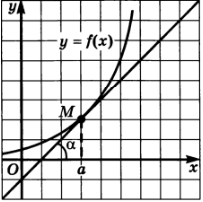
На рисунке изображен график некоторой дифференцируемой функции y = f(x) , которая возрастает. Проведем касательные к графику в точках x_1 и x_2 . Что можно заметить? В обеих точках касательные образуют с осью x острые углы, что говорит о положительном угловом коэффициенте касательных.

Этот угловой коэффициент является значением производной функции в точках касания. Таким образом, f'(x_1) \gt 0 и f'(x_2) \gt 0 . В точке x = 0 касательная совпадает с осью x , что означает, что f'(0) = 0 .

Вообще, для любой возрастающей функции f(x) , определенной на некотором интервале, выполняется условие:

f'(x) \geqslant 0

Убывание функции

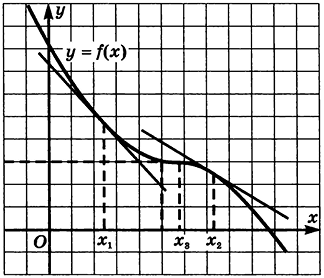
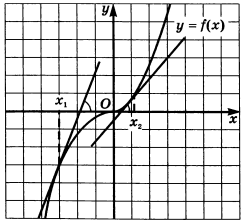
На рисунке представлен график убывающей функции y = f(x) . Аналогично проведем касательные в точках x_1 и x_2 . Что можно заметить? Обе касательные образуют с осью x тупые углы, что указывает на отрицательный угловой коэффициент.

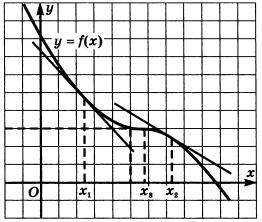
Так как угловой коэффициент касательной равен значению производной, получаем, что f'(x_1) \lt 0 и f'(x_2) \lt 0 . В точке x_3 касательная параллельна оси x , и производная в этой точке равна нулю: f'(x_3) = 0 .

Для любой убывающей функции f(x) справедливо следующее условие:

f'(x) \leqslant 0

Выводы о монотонности функции

Таким образом, существует четкая связь между знаком производной функции и ее монотонностью:

1. Если функция возрастает на интервале и имеет производную на этом интервале, то f'(x) \geqslant 0 .
2. Если функция убывает, то f'(x) \leqslant 0 .

Однако важным является и обратное утверждение: если на интервале производная положительна, функция возрастает, если производная отрицательна — функция убывает. Это дает возможность анализировать поведение функции, не строя её график, а лишь исследовав производную.

Теорема 1

Если на интервале X для всех x выполняется f'(x) \geqslant 0 , и при этом равенство f'(x) = 0 выполняется лишь в конечном числе точек, то функция y = f(x) возрастает на интервале X .

Теорема 2

Если на интервале X для всех x выполняется f'(x) \lt 0 , и при этом равенство f'(x) = 0 либо не выполняется, либо выполняется лишь в отдельных точках, то функция y = f(x) убывает на этом интервале.

Физическая интерпретация

Производная функции имеет также физический смысл. Представим себе движение точки по прямой, описываемое функцией s = s(t) , где s(t) — закон движения. Если скорость положительна, то точка удаляется от начала отсчета, и функция s(t) возрастает. Если скорость отрицательна, то точка приближается к началу отсчета, и функция s(t) убывает. Таким образом, производная (скорость) определяет поведение функции.

Пример 1.

Доказать, что функция y = x^5 + 2x^3 - 4 возрастает на всей числовой прямой.

Решение. Найдем производную функции:

f'(x) = 5x^4 + 6x^2

Заметим, что при всех x данная производная неотрицательна ( f'(x) \geqslant 0 ), причем равенство f'(x) = 0 выполняется только в точке x = 0 . Следовательно, по теореме 1, функция возрастает на всей числовой прямой.

Пример 2.

а) Исследовать на монотонность функцию y = 2x^3 + 3x^2 - 1 .
б) Построить график этой функции.

Решение:

а) Для исследования на монотонность, найдем производную:

y' = 6x^2 + 6x = 6x(x + 1)

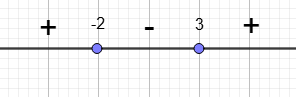
Рассмотрим знак производной на различных интервалах:

• На интервале (- \infty; -1) производная положительна, значит, функция возрастает.
• На интервале (-1; 0) производная отрицательна, следовательно, функция убывает.
• На интервале (0; +\infty) производная снова положительна, функция возрастает.

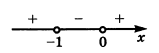
Таким образом, функция возрастает на интервале (- \infty; -1] , убывает на [-1; 0] , и снова возрастает на [0; +\infty) .

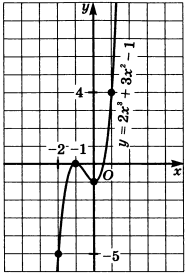
б) Для построения графика составим таблицу значений функции в ключевых точках.

x	-1	0	1	-2
y	0	-1	4	-5

Отметим эти точки на координатной плоскости и учтем промежутки возрастания и убывания, а также параллельность касательной оси x в точках x = -1 и x = 0 .

Постоянные функции

Если на всем промежутке производная функции тождественно равна нулю, то функция ни возрастает, ни убывает. Это постоянная функция.

Теорема 3

Если на интервале X f'(x) = 0 для всех x , то функция y = f(x) постоянна на этом интервале.

y=\cos x+2 x ;

Производная неотрицательна при

x \in R :

y^{\prime}(x)=(\cos x)^{\prime}+(2 x)^{\prime}=

-\sin x+2 \gt 0 ;

| \sin x |\leq 1,

(2-\sin x) \geq 1 ;

y=x^5+3 x^3+7 x+4

Производная неотрицательна при x \in R :

y^{\prime}(x)=\Big(x^5\Big)^{\prime}+3\Big(x^3\Big)^{\prime}+(7 x+4)^{\prime}

y^{\prime}(x)=5 x^4+3 \cdot 3 x^2+7=

5 x^4+9 x^2+7 \gt 0 ; \\ x^4 \geq 0, \quad x^2 \geq 0 ; \leq{n}

y=x^5+4 x^3+8 x-8

Производная неотрицательна при x \in R :

y^{\prime}(x)=\Big(x^5\Big)^{\prime}+4\Big(x^3\Big)^{\prime}+(8 x-8)^{\prime} ;

y^{\prime}(x)=5 x^4+4 \cdot 3 x^2+8=

5 x^4+12 x^2+8 \gt 0 ;

x^4 \geq 0, \\ x^2 \geq 8 ; \leq{n}

y=x^2-5 x+4

Найдем производную функции:

y'=2x-5

Производная отрицательна на (-\infty ; 2,5) и положительна на (2,5 ;+\infty), значит, на первом из указанных промежутков функция убывает, на втором возрастает.

y=-x^2+8 x-7

Найдем производную функции:

y^{\prime}=-2 x+8

Производная положительна на (-\infty ; 4) и отрицательна на (4 ;+\infty), значит, на первом из указанных промежутков функция возрастает, на втором - убывает.

y=60+45 x-3 x^2-x^3

Найдем производную функции: y^{\prime}=45-6 x-3 x^2

Чтобы найти нули производной, приравняем ее нулю:

\begin{aligned} & 45-6 x-3 x^2=0 \\ & x^2+2 x-15=0 \\ & x_{1,2}=\frac{-2 \pm \sqrt{4+60}}{2}=-1 \pm 4 \\ & x_1=-5, x_2=3 \\ & + \end{aligned}

Функция убывает на (-\infty ;-5) и (3 ;+\infty), возрастает на (-5 ; 3),

y=-x^5+5 x

Найдем производную функции:

y^{\prime}=-5 x^4+5

Чтобы найти нули производной, приравняем ее нулю:

\begin{gathered} -5 x^4+5=0 \\ x^4=1 \\ x= \pm 1 \end{gathered}

функция убывает на (-\infty ;-1) и (1 ;+\infty) , и возрастает на (-1 ; 1)

y=2 x^3-3 x^2-36 x+40

Найдем производную функции:

y^{\prime}=6 x^2-6 x-36

Чтобы найти нули производной, приравняем ее нулю:

6 x^2-6 x-36=0

x^2-x-6=0

x_{1,2}=\frac{1 \pm \sqrt{1+24}}{2}=\frac{1 \pm 5}{2}

x_1=3, x_2=-2

значит функция убывает, на (-2 ; 3) , возрастает на (-\infty ;-2) и (3 ;+\infty)