Арккотангенс и решение уравнения ctg x = a
Введение
Арккотангенс — это обратная функция для котангенса, которая играет важную роль в тригонометрии и позволяет находить угол по известному значению котангенса. В данной статье мы рассмотрим, что такое арккотангенс, его свойства и как решать уравнения вида
Арккотангенс: определение и свойства
Арккотангенс, обозначаемый как
Область определения и значения:
- Область определения функции арккотангенс:
x \in \mathbb{R} (котангенс может принимать любые действительные значения). - Область значений функции арккотангенс:
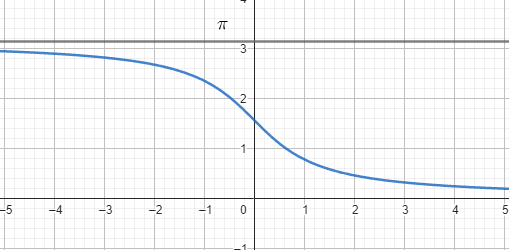
\operatorname{arcctg}(x) \in (0, \pi) . Это значит, что арккотангенс возвращает угол в пределах от 0 до\pi радиан (или от 0° до 180°).
Свойства функции арккотангенс:
- Область определения:
x \in \mathbb{R} . - Область значений:
\operatorname{arcctg}(x) \in (0, \pi) . - Четность: Арккотангенс является нечётной функцией, то есть
\operatorname{arcctg}(-x) = \pi - \operatorname{arcctg}(x) . - Дифференцируемость: Производная арккотангенса равна
\cfrac{-1}{1 + x^2} .
Арккотангенс возвращает основной угол, который лежит в диапазоне от 0 до
Решение уравнения \text{ctg} x = a
Для решения уравнения вида:
где
Основной корень
Основной корень уравнения
Так как котангенс — периодическая функция с периодом
Пример 1: Решение уравнения \text{ctg} x = 1
Найдем решение уравнения
-
Основной корень:
-
Общее решение с учётом периодичности котангенса:
Таким образом, решение уравнения
Пример 2: Решение уравнения \text{ctg} x = -\sqrt{3}
Найдем решение уравнения
-
Основной корень:
-
Общее решение с учётом периодичности:
Таким образом, решение уравнения
Решение уравнения на заданном интервале
В некоторых случаях требуется найти решение уравнения на заданном интервале, например,
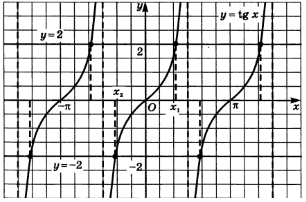
Пример 3: Решение уравнения \text{ctg} x = 2 на интервале [0, 2\pi]
Найдем решение уравнения
-
Основной корень:
-
Следующий корень с учётом периодичности:
Так как мы ищем решения в пределах
Таким образом, решения на интервале