Формулы приведения в тригонометрии

Введение

Формулы приведения играют важную роль в упрощении выражений с тригонометрическими функциями. Они позволяют свести сложные выражения к более простым, в которых аргумент тригонометрической функции выражен через одну переменную. Это значительно облегчает расчёты и решение задач в тригонометрии и математическом анализе. В этой статье мы рассмотрим основные формулы приведения, объясним их происхождение и дадим практические рекомендации по их запоминанию с помощью мнемонических правил.

Определение и смысл формул приведения

Формулы приведения позволяют преобразовывать тригонометрические выражения, содержащие аргументы вида \cfrac{\pi}{2} \pm t , \pi \pm t , \cfrac{3\pi}{2} \pm t и подобные. Любое выражение такого типа можно записать в более простой форме, в которой под знаком тригонометрической функции будет содержаться лишь аргумент t . Эти преобразования основаны на периодичности и симметрии тригонометрических функций.

Для понимания сути формул приведения вспомним основные свойства тригонометрических функций, такие как их чётность/нечётность и периодичность:

• Синус — нечётная функция: \sin(-t) = -\sin(t) .
• Косинус — чётная функция: \cos(-t) = \cos(t) .
• Период синуса и косинуса равен 2\pi : \sin(t + 2\pi) = \sin(t) и \cos(t + 2\pi) = \cos(t) .
• Тангенс и котангенс также являются периодическими функциями с периодом \pi : \tg(t + \pi) = \tg(t) и \ctg(t + \pi) = \ctg(t) .

Основные формулы приведения

Рассмотрим ключевые формулы приведения, которые применяются для преобразования выражений с синусом, косинусом, тангенсом и котангенсом.

Формулы приведения для синуса и косинуса

Формулы приведения для синуса и косинуса можно рассмотреть на примере выражений вида \pi \pm t и \cfrac{\pi}{2} \pm t .

1. Синус:
   \sin(\pi + t) = -\sin t
   Эта формула выводится из периодичности синуса и его нечётности. Поскольку синус имеет период 2\pi , прибавление \pi меняет знак функции.

2. Косинус:
   \cos(\pi + t) = -\cos t
   Косинус, подобно синусу, изменяет знак при прибавлении \pi , что связано с его периодом и симметрией относительно оси ординат.

3. Синус с добавлением половины периода:
   \sin\Big(\cfrac{\pi}{2} + t\Big) = \cos t
   Эта формула основана на том, что синус и косинус связаны сдвигом аргумента на \cfrac{\pi}{2} : синус превращается в косинус и наоборот.

4. Косинус с добавлением половины периода:
   \cos\Big(\cfrac{\pi}{2} + t\Big) = -\sin t
   Здесь мы видим обратную связь: при добавлении \cfrac{\pi}{2} к косинусу, он превращается в синус, но с противоположным знаком.

Формулы приведения для тангенса и котангенса

Для тангенса и котангенса также существуют простые правила:

1. Тангенс:
   \tg(\pi + t) = \tg t
   Поскольку тангенс является периодической функцией с периодом \pi , прибавление \pi не изменяет его значения.

2. Котангенс:
   \ctg(\pi + t) = \ctg t
   Котангенс, аналогично тангенсу, не изменяет своего значения при прибавлении периода \pi .

Примеры других формул приведения

Используя базовые формулы и свойства тригонометрических функций, можно вывести и другие формулы приведения. Приведем несколько примеров.

1. Синус с добавлением трёх четвертей периода:
   \sin\Big(\cfrac{3\pi}{2} + t\Big) = -\cos t
   Это выражение можно получить, рассматривая преобразование \sin\Big(\cfrac{3\pi}{2} + t\Big) как сумму \pi + \Big(\cfrac{\pi}{2} + t\Big) и применяя формулы приведения поэтапно.

2. Косинус с вычитанием аргумента:
   \cos(\pi - t) = -\cos t
   Этот результат выводится из того, что вычитание аргумента эквивалентно добавлению отрицательного значения, что меняет знак косинуса.

Таблицы формул приведения и их использование

Вместо того чтобы выводить формулы приведения каждый раз заново, можно использовать таблицы, в которых указаны основные преобразования для различных тригонометрических функций. Однако такие таблицы могут быть довольно громоздкими, особенно когда необходимо учесть все возможные варианты выражений. Поэтому на практике часто используют мнемонические правила для запоминания основных формул.

Мнемоническое правило для запоминания формул приведения

Чтобы легко запомнить формулы приведения, существует простое мнемоническое правило. Оно заключается в следующем:

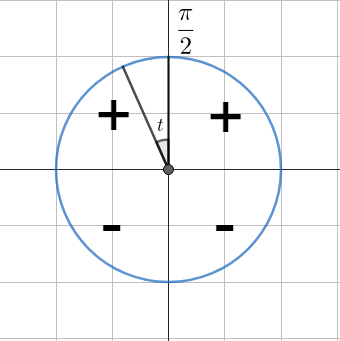
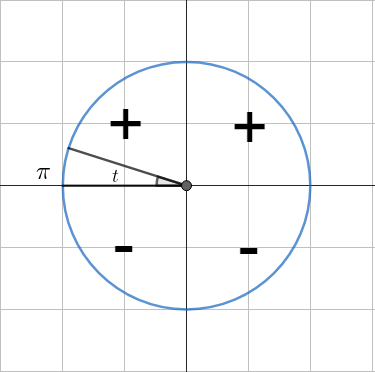
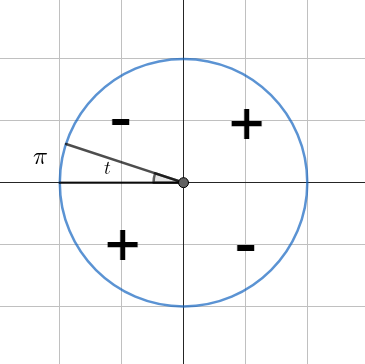
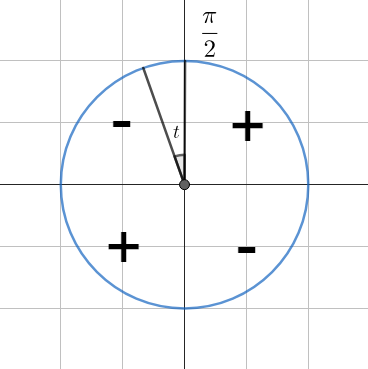
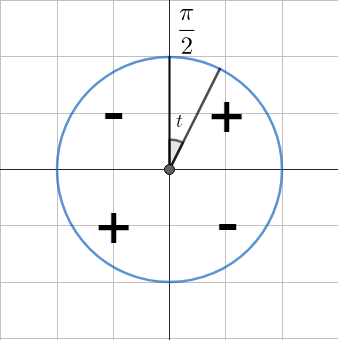
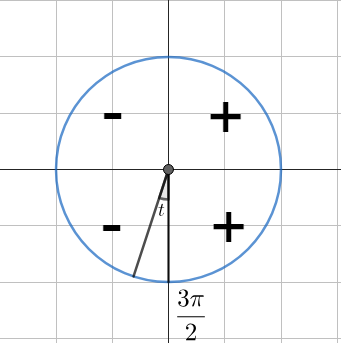
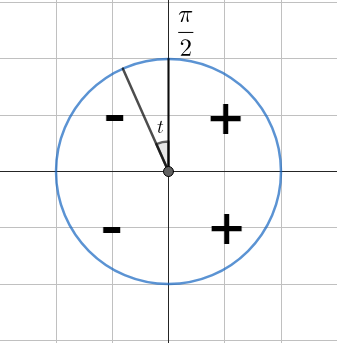
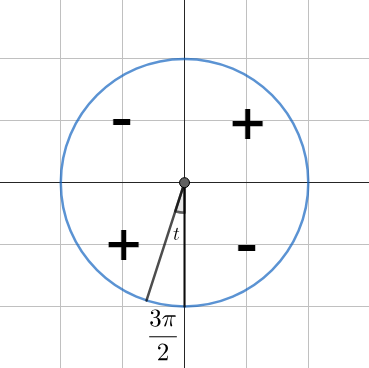
1. Определяем четверть. В зависимости от того, в какой четверти находится угол, определяем знак функции.

   • В первой четверти ( 0 \lt t \lt \cfrac{\pi}{2} ) все функции положительны.
   • Во второй четверти ( \cfrac{\pi}{2} \lt t \lt \pi ) синус положителен, остальные функции отрицательны.
   • В третьей четверти ( \pi \lt t \lt \cfrac{3\pi}{2} ) положителен только тангенс.
   • В четвёртой четверти ( \cfrac{3\pi}{2} \lt t \lt 2\pi ) положителен косинус.

2. Преобразуем функцию. Если аргумент тригонометрической функции содержит \cfrac{\pi}{2} или \cfrac{3\pi}{2} , меняем функцию на её сопряжённую:

   • \sin меняется на \cos и наоборот.
   • \tg меняется на \ctg и наоборот.

3. Определяем знак. Для каждого случая проверяем, какой знак будет у функции, используя информацию о четверти, в которой находится угол.

Заключение

Формулы приведения — важный инструмент в тригонометрии, который позволяет существенно упростить вычисления. Знание этих формул и умение их применять позволяет быстрее и точнее решать задачи, связанные с тригонометрическими функциями. Несмотря на обилие формул, их легко запомнить, используя мнемонические правила и понимание базовых свойств тригонометрических функций.

• Если содержится выражение \pi \pm t или 2 \pi \pm t. Наименование тригонометрической функции следует сохранить

• Если содержится выражение \cfrac{\pi}{2} \pm t, \cfrac{3 \pi}{2}\pm t, то наименование тригонометрической функции следует изменить на родственное (синус - на косинус, косинус на синус, тангенс - на котангенс, котангенс - на тангенс)

• Перед полученной функцией от аргумента t надо поставить тот знак, который имела бы преобразуемая функция при условии, что 0 \lt t \lt \cfrac{\pi}{2}.

\sin (\pi+t) =-\sin t
\cos (\pi+t) =-\cos t \sin t{n}\cos t{n}

Основные формулы

\sin \left(\cfrac{\pi}{2}+t\right) =\cos t

\cos \left(\cfrac{\pi}{2}+t\right) =-\sin t

-\cos t{n}\sin t{n}

\text{tg}(\pi+t) =\text{tg} t
\text{ctg}(\pi+t) =\text{ctg} t -\text{tg} t{n}-\text{ctg} t{n}

\sin \Big(\cfrac{\pi}{2}+t\Big)= \cos t -\sin t {n} -\cos t {n} \sin t {n}

\sin (\pi-t)= \sin t -\sin t {n} -\cos t {n} \cos t {n}

\operatorname{tg} (\pi-t)= -\operatorname{tg} t

\operatorname{ctg} t {n} -\operatorname{ctg} t {n} \operatorname{tg} t {n}

\operatorname{ctg} \Big(\cfrac{\pi}{2}+t\Big)= -\operatorname{tg} t \operatorname{ctg} t {n} -\operatorname{ctg} t {n} \operatorname{tg} t {n}

\operatorname{tg} \Big(\cfrac{\pi}{2}-t\Big)= \operatorname{ctg} t -\operatorname{ctg} t {n} \operatorname{tg} t {n} -\operatorname{tg} t {n}

\cos \Big(\cfrac{3\pi}{2}-t\Big)= -\sin t -\cos t {n} \sin t {n} \cos t {n}

\cos \Big(\cfrac{\pi}{2}+t\Big)= -\sin t -\cos t {n} \sin t {n} \cos t {n}

\operatorname{ctg}\Big(\cfrac{3 \pi}{2}-t\Big)= \operatorname{tg} t -\operatorname{tg} t {n} \operatorname{ctg} t {n} -\operatorname{ctg} t {n}

Уростите

\cfrac{\cos(\pi-t)+\cos\!\left(\cfrac{\pi}{2}-t\right)}{\sin\left(2\pi-t\right)-\sin\!\left(\cfrac{3\pi}{2}-t\right)}=

{\cfrac{-\cos t+\sin t }{-\sin t+\cos\ t}}=-1

Используя предыдущие свойства, можно вывести ряд других формул приведения.

\cos (\pi-t)=\cos (\pi+(-t))=

-\cos (-t)=-\cos t

Используя предыдущие свойства, можно вывести ряд других формул приведения

\sin \Big(\cfrac{3 \pi}{2}+t\Big)=

\sin \Big(\pi+\Big(\cfrac{\pi}{2}+t\Big)\Big)=

-\sin\Big(\cfrac{\pi}{2}+t\Big)= -\cos t

\cfrac{\cos(180^{\circ}+\alpha)\cos(-\alpha)}{\sin\big(-\alpha\mathrm{)sin}\big(90^{\circ}+\alpha\big)}=

\cfrac{-\cos(\alpha)\cos(\alpha)} {-\sin\left(\alpha\right)\cos(\alpha)}=\operatorname{ctg} \alpha

\sin \Big(\cfrac{3 \pi}{2}-t\Big)=

\sin \Big(\pi+\cfrac{\pi}{2}-t\Big)=

-\sin \Big(\cfrac{\pi}{2}-t\Big)=

-\cos (-t)=-\cos t3\pi{n}

\cos \Big(90^{\circ}-\alpha\Big)= -\sin (-\alpha)=\sin \alpha

\operatorname{tg}\Big(\cfrac{3 \pi}{2}+t\Big)=

\operatorname{tg}\Big(\pi+\cfrac{\pi}{2}+t\Big)=

\operatorname{tg}\Big(\cfrac{\pi}{2}+t\Big) =-\operatorname{ctg} t

\operatorname{tg} 300^{\circ}=\operatorname{tg}\Big(360^{\circ}-60^{\circ}\Big)=

\operatorname{tg}\Big(-60^{\circ}\Big)=-\operatorname{tg}60^{\circ}=-\sqrt{3}

\cos 330^{\circ}=\cos \Big(360^{\circ}-30^{\circ}\Big)=

\cos \Big(-30^{\circ}\Big)=

\cos 30^{\circ}=\cfrac{\sqrt{3}}{2}

1{n} 3{n} \sqrt{2}{n}

\operatorname{ctg} 315^{\circ}=\operatorname{ctg}\Big(360^{\circ}-45^{\circ}\Big)=\\\operatorname{ctg}\Big(-45^{\circ}\Big)=-\operatorname{ctg} 45^{\circ}=-1

Найдите значение

\sin \Big(-\cfrac{11 \pi}{6}\Big)=-\sin \cfrac{11 \pi}{6}=

-\sin \Big(2 \pi-\cfrac{\pi}{6}\Big)=

\sin \Big(\cfrac{\pi}{6}\Big)=\cfrac{1}{2}

\sin \cfrac{7 \pi}{6}=

\sin \Big(\pi+\cfrac{\pi}{6}\Big)=

-\sin \cfrac{\pi}{6}=-\cfrac{1}{2}

3{n} 4{n} \sqrt{2}{n}