1\. Задачи, приводящие к понятию производной
Часто в разных задачах, на первый взгляд далеких друг от друга, мы приходим к схожим математическим моделям. Это является одной из сильных сторон математики: разработанные методы для одной модели могут применяться в самых разных областях знаний. Вы уже умеете работать с различными математическими моделями, такими как уравнения, неравенства и системы уравнений. В данном параграфе будет рассмотрена новая для вас математическая модель. Рассмотрим две задачи: одну из физики и одну из геометрии. Процесс их решения приведет нас к новой математической модели.
Задача 1 (о скорости движения)
Тело движется вдоль прямой, на которой задано начало отсчета и направление. Закон движения тела описывается функцией
Решение
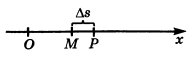
Пусть в момент времени
Средняя скорость тела за интервал времени
Теперь определим мгновенную скорость
Определение касательной к кривой
Прежде чем перейти ко второй задаче, разберемся, что такое касательная к плоской кривой. В школьной программе мы уже встречались с понятием касательной, например, к параболе
Чтобы формализовать понятие касательной, рассмотрим кривую
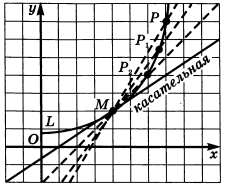
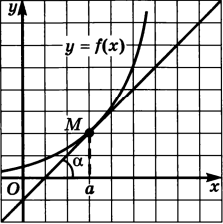
Задача 2 (о касательной к графику функции)
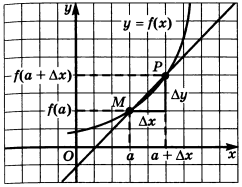
Дан график функции
Решение
Для этого введем приращение
При устремлении
2\. Определение производной
Теперь, когда мы сформировали интуитивное понимание производной, дадим её формальное определение.
Определение
Пусть функция
Для обозначения производной также используют символы
Физический и геометрический смысл производной
Производная имеет несколько интерпретаций. Рассмотрим две из них:
-
Физический смысл. В физике производная функции положения по времени
s'(t) интерпретируется как мгновенная скорость движения тела в момент времениt :
-
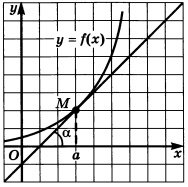
Геометрический смысл. Угловой коэффициент касательной к графику функции
y = f(x) в точкеx = a равен значению производной в этой точке:
Алгоритм нахождения производной
Для нахождения производной функции
- Найти значение функции в точке
x . - Рассчитать приращение функции
\Delta y = f(x + \Delta x) - f(x) . - Составить отношение
\cfrac{\Delta y}{\Delta x} . - Найти предел при
\Delta x \to 0 .
Пример 1. Найти производную постоянной функции y = C .
Решение:
Пример 2. Найти производную функции y = \cfrac{1}{x} .
Решение:
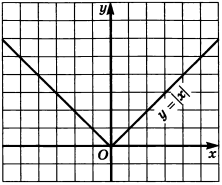
Непрерывность и дифференцируемость
Если функция
Итог
Производная функции играет ключевую роль в математике и её приложениях. Она позволяет исследовать скорость изменений процессов в физике, экономике и других науках, а также даёт геометрическое представление углового коэффициента касательной к графику функции.