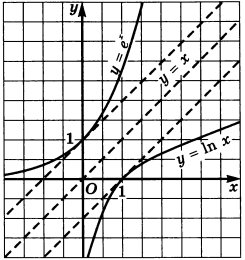
Мы знаем, что график логарифмической функции

Мы знаем, что график логарифмической функции
В курсе математического анализа доказано, что для любого значения
Найти производную
Вспомним
Пусть дана показательная функция
Итак,
Пусть дана логарифмическая функция
Провести касательную к графику функции
Воспользуемся алгоритмом составления уравнения касательной к графику функции, учитывая, что в данном примере
Подставим найденные числа
Получим:
Значение функции:
Значение производной:
Уравнение касательной:
Значение функции:
Значение производной:
Уравнение касательной:
.
Значение функции:
Значение производной:
Уравнение касательной: