Определение основных тригонометрических функций
Определение 1: Синус и косинус
.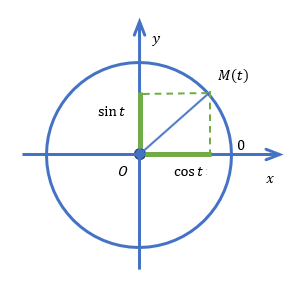
Рассмотрим числовую окружность, где точка
Отсюда следует, что значения синуса и косинуса всегда лежат в пределах от -1 до 1:
Определение 2: Тангенс и котангенс
Тангенс числа
Котангенс числа
Важно помнить, что тангенс и котангенс определены только при тех значениях
\operatorname{tg} t существует при\cos t \neq 0 \operatorname{ctg} t существует при\sin t \neq 0
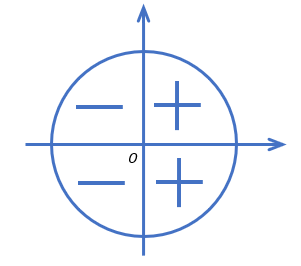
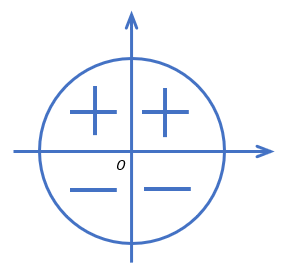
Знаки тригонометрических функций по четвертям
Числовая окружность делится на четыре четверти, и в каждой из них координаты
- I четверть:
x \gt; 0 ,y \gt; 0 - II четверть:
x \lt; 0 ,y \gt; 0 - III четверть:
x \lt; 0 ,y \lt; 0 - IV четверть:
x \gt; 0 ,y \lt; 0
Это позволяет составить таблицу знаков тригонометрических функций по четвертям:
| Четверть | |||
|---|---|---|---|
| I | + | + | + |
| II | - | + | - |
| III | - | - | + |
| IV | + | - | - |
Основное тригонометрическое тождество
Уравнение числовой окружности записывается как:
Подставляя выражения для
Таблицы значений тригонометрических функций
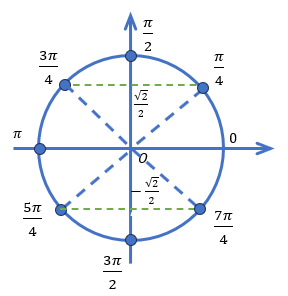
Значения синуса и косинуса для некоторых характерных углов приведены в таблицах:
Таблица 1: Значения синуса и косинуса
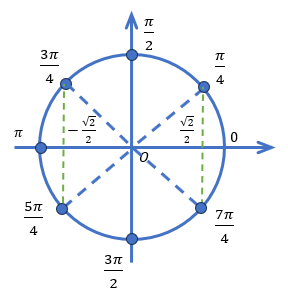
| 1 | 0 | -1 | 0 | 1 | |||||
| 0 | 1 | 0 | -1 | 0 |
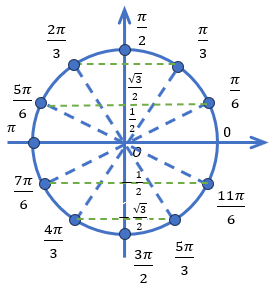
Таблица 2: Дополнительные значения для \cfrac{\pi}{6} и \cfrac{\pi}{3}
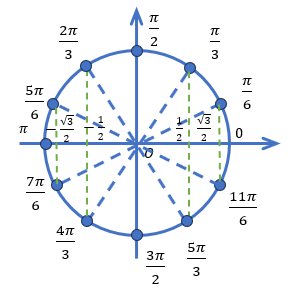
Таблица 3: Значения тангенса и котангенса
| 0 | 1 | - | |||
| - | 1 | 0 |
Примеры решения задач
Пример 1: Вычислить \cos t и \sin t
-
Для
t = \cfrac{45 \pi}{4} :t = \cfrac{45 \pi}{4} соответствует\cfrac{5 \pi}{4} . Из таблиц получаем:\cos \cfrac{45 \pi}{4} = -\cfrac{\sqrt{2}}{2}, \quad \sin \cfrac{45 \pi}{4} = -\cfrac{\sqrt{2}}{2} -
Для
t = -\cfrac{37 \pi}{3} : Это значение эквивалентноt = \cfrac{5 \pi}{3} . Используя таблицы:\cos \Big(-\cfrac{37 \pi}{3}\Big) = \cfrac{1}{2}, \quad \sin \Big(-\cfrac{37 \pi}{3}\Big) = -\cfrac{\sqrt{3}}{2}
Пример 2: Решить уравнение \sin t = \cfrac{1}{2}
Нам нужно найти все значения
Заключение
В данном параграфе рассмотрены основные тригонометрические функции: синус, косинус, тангенс и котангенс. Они связаны друг с другом и описываются через значения координат точек числовой окружности. Составлены таблицы значений для некоторых характерных углов, а также рассмотрены примеры решения уравнений и неравенств, содержащих тригонометрические функции.