Тест по теме: Методы решения тригонометрических уравнений

Общие сведения о тригонометрических уравнениях

Тригонометрические уравнения — это уравнения, которые включают тригонометрические функции, такие как синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Решение таких уравнений заключается в нахождении всех значений углов, при которых тригонометрическая функция принимает заданное значение.

Общие решения тригонометрических уравнений

Для решения базовых тригонометрических уравнений \sin x = a , \cos x = a , \operatorname{tg} x = a , \operatorname{ctg} x = a существуют общие формулы, которые позволяют найти все решения. Рассмотрим их:

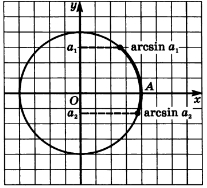
• \sin x = a :
  x = (-1)^n \arcsin a + \pi n, \quad n \in \mathbb{Z}

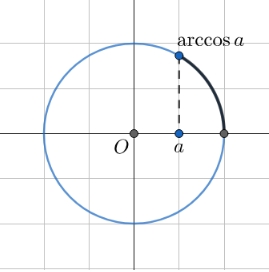
• \cos x = a :
  x = \pm \arccos a + 2\pi n, \quad n \in \mathbb{Z}

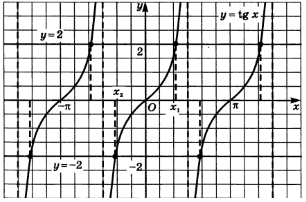
• \operatorname{tg} x = a :
  x = \text{arctg} a + \pi n, \quad n \in \mathbb{Z}

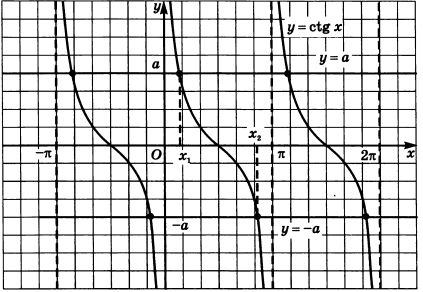
• \operatorname{ctg} x = a :
  x = \text{arcctg} a + \pi n, \quad n \in \mathbb{Z}

Теперь перейдем к рассмотрению основных методов решения тригонометрических уравнений.

Метод приведения к базовому тригонометрическому уравнению

Один из самых распространенных методов решения тригонометрических уравнений — это приведение уравнения к одному из базовых вида: \sin x = a , \cos x = a , \operatorname{tg} x = a , \operatorname{x} = a .

Пример 1

Решим уравнение:
2\sin x - 1 = 0.

Шаг 1. Приведение к простому уравнению:

Переносим «1» в правую часть и делим обе части на 2:
\sin x = \cfrac{1}{2}.

Шаг 2. Поиск решений:

Из таблицы значений тригонометрических функций известно, что \sin x = \cfrac{1}{2} при x = \cfrac{\pi}{6} и x = \cfrac{5\pi}{6} .

Общее решение будет иметь вид:
x = \cfrac{\pi}{6} + 2\pi n \quad \text{или} \quad x = \cfrac{5\pi}{6} + 2\pi n, \quad n \in \mathbb{Z}.

Метод использования тригонометрических тождеств

Многие тригонометрические уравнения можно решить, используя известные тригонометрические тождества. Приведем несколько часто используемых тождеств:

• Основное тригонометрическое тождество:
  \sin^2 x + \cos^2 x = 1.

• Тождество для тангенса и котангенса:
  \operatorname{tg} x \cdot \operatorname{ctg} x = 1.

Пример 2

Решим уравнение:
\sin^2 x = \cos x.

Шаг 1. Применение тождества:

Из основного тригонометрического тождества \sin^2 x = 1 - \cos^2 x , подставим его в уравнение:
1 - \cos^2 x = \cos x.

Шаг 2. Преобразование уравнения:

Переносим все слагаемые в одну часть уравнения:
\cos^2 x + \cos x - 1 = 0.

Шаг 3. Решение квадратного уравнения:

Это квадратное уравнение относительно \cos x . Используем дискриминант:
D = 1^2 - 4 \cdot 1 \cdot (-1) = 1 + 4 = 5.
Корни уравнения:
\cos x = \cfrac{-1 + \sqrt{5}}{2}, \quad \cos x = \cfrac{-1 - \sqrt{5}}{2}.

Значение \cos x = \cfrac{-1 - \sqrt{5}}{2} не удовлетворяет условию -1 \leq \cos x \leq 1 , поэтому оставляем только \cos x = \cfrac{-1 + \sqrt{5}}{2} .

Решаем уравнение:
x = \pm \arccos \Big( \cfrac{-1 + \sqrt{5}}{2} \Big) + 2\pi n, \quad n \in \mathbb{Z}.

Метод разложения на множители

Иногда тригонометрические уравнения могут быть представлены в виде произведения множителей, что упрощает процесс их решения.

Пример 3

Решим уравнение:
\sin x \cdot (2\cos x - 1) = 0.

Шаг 1. Разбиение на два уравнения:

Произведение равно нулю, если хотя бы один из множителей равен нулю:

1. \sin x = 0 ,
2. 2\cos x - 1 = 0 .

Шаг 2. Решение первого уравнения:

\sin x = 0 \quad \Rightarrow \quad x = \pi n, \quad n \in \mathbb{Z}.

Шаг 3. Решение второго уравнения:

2\cos x - 1 = 0 \quad \Rightarrow \quad \cos x = \cfrac{1}{2}.
Из таблицы значений тригонометрических функций:
x = \pm \cfrac{\pi}{3} + 2\pi n, \quad n \in \mathbb{Z}.

Шаг 4. Общее решение:

Таким образом, общее решение будет состоять из двух частей:
x = \pi n \quad \text{или} \quad x = \pm \cfrac{\pi}{3} + 2\pi n, \quad n \in \mathbb{Z}.

Метод замены переменной

В некоторых случаях решение уравнения можно упростить с помощью замены переменной.

Пример 4

Решим уравнение:
2\sin^2 x + 3\sin x - 2 = 0.

Шаг 1. Замена переменной:

Обозначим \sin x = t , тогда уравнение примет вид:
2t^2 + 3t - 2 = 0.

Шаг 2. Решение квадратного уравнения:

Решаем квадратное уравнение относительно t :
D = 3^2 - 4 \cdot 2 \cdot (-2) = 9 + 16 = 25,

t_1 = \cfrac{-3 + 5}{4} = \cfrac{1}{2}, \quad t_2 = \cfrac{-3 - 5}{4} = -2.

Шаг 3. Возвращение к тригонометрической функции:

1. \sin x = \cfrac{1}{2} :
   x = \cfrac{\pi}{6} + 2\pi n \quad \text{или} \quad x = \cfrac{5\pi}{6} + 2\pi n, \quad n \in \mathbb{Z}.

2. \sin x = -2 не имеет решений, так как \sin x лежит в пределах от -1 до 1.

Шаг 4. Общее решение:

Таким образом, общее решение:
x = \cfrac{\pi}{6} + 2\pi n \quad \text{или} \quad x = \cfrac{5\pi}{6} + 2\pi n, \quad n \in \mathbb{Z}.

Заключение

Мы рассмотрели основные методы решения тригонометрических уравнений: приведение к базовому уравнению, использование тригонометрических тождеств, разложение на множители и метод замены переменной. Важно уметь применять каждый из этих методов в зависимости от структуры уравнения.

2 \sin ^2 x-5 \sin x+2=0 ;

Введем новую переменную z=\sin x .

Тогда уравнение примет вид 2 z^2-5 z+2=0 , откуда находим:

z_1=2, z_2=\cfrac{1}{2} .

Значит, либо \sin x=2 , либо \sin x=\cfrac{1}{2} .

Первое уравнение не имеет корней, а из второго находим:

x=(-1)^n \arcsin \cfrac{1}{2}+\pi n ;\\ x=(-1)^n \cfrac{\pi}{6}+\pi n .

\cos ^2 x-\sin ^2 x-\cos x=0 .

Воспользуемся тем, что \cos ^2 x=1-\cos ^2 x .
Тогда заданное уравнение можно переписать в виде

\cos ^2 x-\Big(1-\cos ^2 x\Big)-\cos x=0 .

После понятных преобразований получим:

2 \cos ^2 x-\cos x-1=0 .

Введем новую переменную:

z=\cos x .
Тогда уравнение примет вид

2 z^2-z-1=0 ,

откуда находим: z_1=1, z_2=-\cfrac{1}{2} .

Значит, либо \cos x=1 , либо \cos x=-\cfrac{1}{2} .

Из первого уравнения находим: x=2 \pi n ;

из второго уравнения находим:

x= \pm \arccos \Big(-\cfrac{1}{2}\Big)+2 \pi n ; x= \pm \cfrac{2 \pi}{3}+2 \pi n .

\Big(\sin x-\cfrac{1}{3}\Big)\Big(\cos x+\cfrac{2}{5}\Big)=0.

Решение. Задача сводится к решению совокупности уравнений:

\sin x=\cfrac{1}{3} ;

\cos x=-\cfrac{2}{5} .

Из этих уравнений находим соответственно:

x=(-1)^n \arcsin \cfrac{1}{3}+\pi n ; \quad

x= \pm \arccos \Big(-\cfrac{2}{5}\Big)+2 \pi n .

2 \sin \cfrac{x}{2} \cos 5 x-\cos 5 x=0 .
Имеем: \cos 5 x\Big(2 \sin \cfrac{x}{2}-1\Big)=0 .

Значит, приходим к совокупности уравнений

\cos 5 x=0 ; \quad \sin \cfrac{x}{2}=\cfrac{1}{2} .

Из первого уравнения находим:

5 x=\cfrac{\pi}{2}+\pi n ; x=\cfrac{\pi}{10}+\cfrac{\pi n}{5} .

Из второго уравнения находим:

\cfrac{x}{2}=(-1)^n \cfrac{\pi}{6}+\pi n ; x=(-1)^n \cfrac{\pi}{3}+ +2 \pi n .

3 \sin ^2 x-5 \sin x-2=0
Пусть y=\sin x
тогда: 3 y^2-5 y-2=0 ; \\ D=5^2+4 \cdot 3 \cdot 2=25+24=49, \text { тогда: } \\ y_1=\cfrac{5-7}{2 \cdot 3}=-\cfrac{2}{6}=-\cfrac{1}{3} \text { и } \\ y_2=\cfrac{5+7}{2 \cdot 3}=\cfrac{12}{6}=2 ;

Первое значение: \sin x=-\cfrac{1}{3} ; \\ x=(-1)^{n+1} \cdot \arcsin \cfrac{1}{3}+\pi n ;

Второе значение:
\sin x=2 \gt 1 ; \\ x \in \emptyset ;

Ответ: (-1)^{n+1} \cdot \arcsin \cfrac{1}{3}+\pi n .

2 \sin ^2 \cfrac{x}{2}-3 \sin \cfrac{x}{2}+1=0

Пусть y=\sin \cfrac{x}{2}
тогда:
2 y^2-3 y+1=0 ;

D=3^2-4 \cdot 2=9-8=1, \text { тогда: }

y\_1=\cfrac{3-1}{2 \cdot 2}=\cfrac{2}{4}=\cfrac{1}{2} \text { и } y\_2=\cfrac{3+1}{2 \cdot 2}=\cfrac{4}{4}=1 ;

Первое значение:

\sin \cfrac{x}{2}=\cfrac{1}{2} ;

\cfrac{x}{2}=(-1)^n \cdot \arcsin \cfrac{1}{2}+\pi n=(-1)^n \cdot \cfrac{\pi}{6}+\pi n ;

x=(-1)^n \cdot \cfrac{\pi}{3}+2 \pi n ;

Второе значение:

\sin \cfrac{x}{2}=1 ;

\cfrac{x}{2}=\cfrac{\pi}{2}+2 \pi n

x=\pi+4 \pi n ;

\text { ответ: }(-1)^n \cdot \cfrac{\pi}{3}+2 \pi n ; \pi+4 \pi n .