Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения — это уравнения, которые содержат тригонометрические функции (синус, косинус, тангенс, котангенс) и приводятся к стандартным формам для нахождения их решений. В данной статье рассмотрим основные типы таких уравнений и приведем примеры их решения.
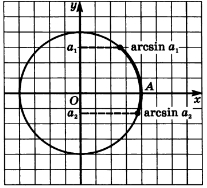
Уравнение sin x = a
Уравнение вида \sin x = a , где a \in [-1, 1] , решается следующим образом:
x = \arcsin(a) + 2\pi n \quad \text{или}
\quad x = \pi - \arcsin(a) + 2\pi n, \quad n \in \mathbb{Z}.
Пример 1: Решение уравнения \sin x = 0.5
- Найдем основной угол:
x\_0 = \arcsin(0.5) = \cfrac{\pi}{6}.
- Общее решение с учетом периодичности синуса:
x = \cfrac{\pi}{6} + 2\pi n \quad \text{или}
\quad x = \pi - \cfrac{\pi}{6} + 2\pi n = \cfrac{5\pi}{6} + 2\pi n, \quad n \in \mathbb{Z}.
Таким образом, решение уравнения \sin x = 0.5 имеет вид:
x = \cfrac{\pi}{6} + 2\pi n \quad \text{или} \quad x = \cfrac{5\pi}{6} + 2\pi n, \quad n \in \mathbb{Z}.
Пример 2: Решение уравнения \sin x = -0.5
- Основной угол:
x_0 = \arcsin(-0.5) = -\cfrac{\pi}{6}.
- Общее решение:
x = -\cfrac{\pi}{6} + 2\pi n \quad \text{или}
\quad x = \pi + \cfrac{\pi}{6} + 2\pi n = \cfrac{7\pi}{6} + 2\pi n, \quad n \in \mathbb{Z}.
Таким образом, решение уравнения \sin x = -0.5 :
x = -\cfrac{\pi}{6} + 2\pi n \quad \text{или}
\quad x = \cfrac{7\pi}{6} + 2\pi n, \quad n \in \mathbb{Z}.
Уравнение \sin x = a , где |a| \gt 1
Если a \gt 1 или a \lt -1 , то уравнение не имеет решений, так как значение синуса не может превышать 1 по абсолютной величине.
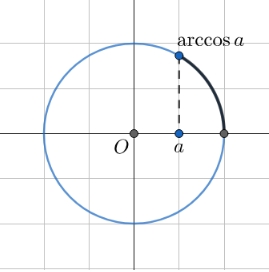
2\. Уравнение \cos x = a
Уравнение \cos x = a , где a \in [-1, 1] , решается следующим образом:
x = \arccos(a) + 2\pi n \quad \text{или}
\quad x = -\arccos(a) + 2\pi n, \quad n \in \mathbb{Z}.
Пример 3: Решение уравнения \cos x = 0.5
- Основной угол:
x_0 = \arccos (\cfrac{1}{2}) = \cfrac{\pi}{3}.
- Общее решение:
x = \cfrac{\pi}{3} + 2\pi n \quad \text{или}
\quad x = -\cfrac{\pi}{3} + 2\pi n = \cfrac{5\pi}{3} + 2\pi n, \quad n \in \mathbb{Z}.
Таким образом, решение уравнения \cos x = 0.5 :
x = \cfrac{\pi}{3} + 2\pi n \quad \text{или}
\quad x = \cfrac{5\pi}{3} + 2\pi n, \quad n \in \mathbb{Z}.
Пример 4: Решение уравнения \cos x = -0.5
- Основной угол:
x_0 = \arccos(-\cfrac{1}{2}) = \cfrac{2\pi}{3}.
- Общее решение:
x = \cfrac{2\pi}{3} + 2\pi n \quad \text{или} \quad
x = -\cfrac{2\pi}{3} + 2\pi n = \cfrac{4\pi}{3} + 2\pi n, \quad n \in \mathbb{Z}.
Таким образом, решение уравнения \cos x = -0.5 :
x = \cfrac{2\pi}{3} + 2\pi n \quad \text{или}
\quad x = \cfrac{4\pi}{3} + 2\pi n, \quad n \in \mathbb{Z}.
Уравнение \cos x = a , где |a| gt; 1
Если a \gt 1 или a \lt -1 , то уравнение не имеет решений, так как значение косинуса не может превышать 1 по абсолютной величине.
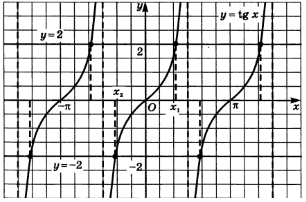
Уравнение tg x = a
Уравнение вида \operatorname{tg} x = a , где a \in \mathbb{R} , решается с использованием арктангенса:
x = \operatorname{arctg}(a) + \pi n, \quad n \in \mathbb{Z}.
Тангенс — периодическая функция с периодом \pi , что учитывается в общем решении.
Пример 5: Решение уравнения \operatorname{tg} x = 1
- Основной угол:
x_0 = \operatorname{arctg}(1) = \cfrac{\pi}{4}.
- Общее решение:
x = \cfrac{\pi}{4} + \pi n, \quad n \in \mathbb{Z}.
Таким образом, решение уравнения \operatorname{tg} x = 1 :
x = \cfrac{\pi}{4} + \pi n, \quad n \in \mathbb{Z}.
Пример 6: Решение уравнения \operatorname{tg} x = -\sqrt{3}
- Основной угол:
x_0 = \operatorname{arctg}(-\sqrt{3}) = -\cfrac{\pi}{3}.
- Общее решение:
x = -\cfrac{\pi}{3} + \pi n, \quad n \in \mathbb{Z}.
Таким образом, решение уравнения \operatorname{tg} x = -\sqrt{3} :
x = -\cfrac{\pi}{3} + \pi n, \quad n \in \mathbb{Z}.
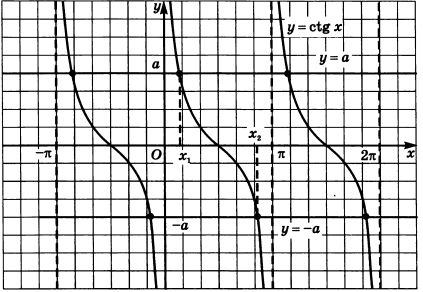
Уравнение \operatorname{ctg} x = a
Уравнение вида \operatorname{ctg} x = a , где a \in \mathbb{R} , решается с использованием арккотангенса:
x = \operatorname{arcctg}(a) + \pi n, \quad n \in \mathbb{Z}.
Котангенс также является периодической функцией с периодом \pi .
Пример 7: Решение уравнения \operatorname{ctg} x = 1
- Основной угол:
x_0 = \operatorname{arcctg}(1) = \cfrac{\pi}{4}.
- Общее решение:
x = \cfrac{\pi}{4} + \pi n, \quad n \in \mathbb{Z}.
Таким образом,
решение уравнения \operatorname{ctg} x = 1 :
x = \cfrac{\pi}{4} + \pi n, \quad n \in \mathbb{Z}.
Пример 8: Решение уравнения \operatorname{ctg} x = -\sqrt{3}
- Основной угол:
x_0 = \operatorname{arcctg}(-\sqrt{3}) = \cfrac{5\pi}{6}.
- Общее решение:
x = \cfrac{5\pi}{6} + \pi n, \quad n \in \mathbb{Z}.
Таким образом, решение уравнения \operatorname{ctg} x = -\sqrt{3} :
x = \cfrac{5\pi}{6} + \pi n, \quad n \in \mathbb{Z}.