Арксинус и решение уравнения sin x = a

Введение

Арксинус является важной функцией в тригонометрии и математике в целом. Это обратная функция для синуса, которая используется для нахождения угла по известному значению синуса. Решение уравнения \sin x = a также связано с арксинусом и требует знания свойств тригонометрических функций и их обратных. В данной статье мы подробно разберём, что такое арксинус, его свойства, и как решать уравнение \sin x = a с примерами.

Арксинус: определение и свойства

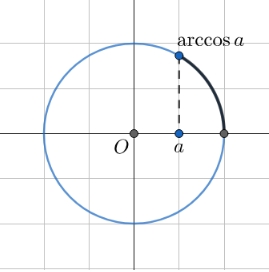
Арксинус, обозначаемый как \arcsin x или \sin^{-1} x , является обратной функцией для синуса. Это означает, что если y = \sin x , то x = \arcsin y .

Область определения и значения:

• Область определения функции арксинус: x \in [-1, 1] , поскольку синус может принимать только значения в этом диапазоне.
• Область значений функции арксинус: \arcsin x \in \Big[ -\cfrac{\pi}{2}, \cfrac{\pi}{2} \Big] , что означает, что арксинус возвращает угол в этом интервале.

Арксинус позволяет найти угол по известному значению синуса в пределах от -\cfrac{\pi}{2} до \cfrac{\pi}{2} , что соответствует первой и четвёртой четвертям на единичной окружности.

Свойства функции арксинус:

1. Область определения: x \in [-1, 1] .
2. Область значений: \arcsin x \in \Big[ -\cfrac{\pi}{2}, \cfrac{\pi}{2} \Big] .
3. Чётность: \arcsin(-x) = -\arcsin(x) (нечётная функция).
4. Дифференцируемость: производная функции арксинус равна \cfrac{1}{\sqrt{1 - x^2}} , для |x| \lt 1 .

Решение уравнения \sin x = a

---

Рассмотрим уравнение вида:

\sin x = a,

где a \in [-1, 1] . Для решения этого уравнения используется функция арксинус, которая даёт основной угол, удовлетворяющий данному уравнению.

Основной корень

Основной корень уравнения \sin x = a — это:

x_0 = \arcsin a.

Однако синус — это периодическая функция, и для полного решения нужно учесть все возможные значения угла, при которых синус равен a .

Общее решение

С учётом периодичности функции синус, общее решение уравнения \sin x = a можно записать следующим образом:

1. Первый набор решений: x_1 = \arcsin a + 2n\pi , где n \in \mathbb{Z} .
2. Второй набор решений: x_2 = \pi - \arcsin a + 2n\pi , где n \in \mathbb{Z} .

Таким образом, общее решение:

x = \arcsin a + 2n\pi \quad \text{или} \quad x = \pi - \arcsin a + 2n\pi, \quad n \in \mathbb{Z}.

Пример 1: Решение уравнения \sin x = \cfrac{1}{2}

Найдем решение уравнения \sin x = \cfrac{1}{2} .

1. Основной корень:

x_0 = \arcsin \cfrac{1}{2} = \cfrac{\pi}{6}.

2. Общее решение:

x_1 = \cfrac{\pi}{6} + 2n\pi \quad \text{и} \quad x\_2 = \pi - \cfrac{\pi}{6} + 2n\pi = \cfrac{5\pi}{6} + 2n\pi.

Таким образом, общее решение:

x = \cfrac{\pi}{6} + 2n\pi \quad \text{или} \quad x = \cfrac{5\pi}{6} + 2n\pi, \quad n \in \mathbb{Z}.

Пример 2: Решение уравнения \sin x = -\cfrac{\sqrt{2}}{2}

Найдем решение уравнения \sin x = -\cfrac{\sqrt{2}}{2} .

1. Основной корень:

x_0 = \arcsin \Big(-\cfrac{\sqrt{2}}{2}\Big) = -\cfrac{\pi}{4}.

2. Общее решение:

x_1 = -\cfrac{\pi}{4} + 2n\pi \quad \text{и} \quad x\_2 = \pi - \Big(-\cfrac{\pi}{4}\Big) + 2n\pi = \cfrac{5\pi}{4} + 2n\pi.

Таким образом, общее решение:

x = -\cfrac{\pi}{4} + 2n\pi \quad \text{или} \quad x = \cfrac{5\pi}{4} + 2n\pi, \quad n \in \mathbb{Z}.

Решение уравнения в заданном интервале

Иногда уравнение требуется решить на определённом интервале, например, x \in [0, 2\pi] . В таких случаях нужно найти значения n , при которых решения попадают в данный интервал.

Пример 3: Решение уравнения \sin x = 0.8 на интервале [0, 2\pi]

1. Основной корень:

x_0 = \arcsin 0.8 \approx 0.927.

2. Общее решение:

x_1 = 0.927 + 2n\pi \quad \text{и} \quad x\_2 = \pi - 0.927 + 2n\pi \approx 2.214 + 2n\pi.

3. Теперь найдём, какие значения x попадают в интервал [0, 2\pi] .

• Для n = 0 , x\_1 \approx 0.927 \in [0, 2\pi] , а x\_2 \approx 2.214 \in [0, 2\pi] .
• Для n = 1 , x_1 \approx 0.927 + 2\pi \approx 7.210 \notin [0, 2\pi] , и аналогично x_2 \approx 2.214 + 2\pi \approx 8.497 \notin [0, 2\pi] .

Таким образом, решения на интервале [0, 2\pi] будут:

x \approx 0.927 \text{и} x \approx 2.214.