Тест по теме: Нахождение наибольшего и наименьшего значений

Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке

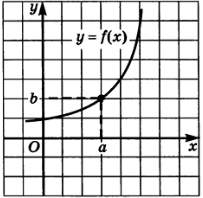
Мы уже знакомы с нахождением наибольшего и наименьшего значений функции через графический анализ. Рассмотрим примеры и теоретические подходы, которые помогут определить экстремумы функций как графически, так и аналитически.

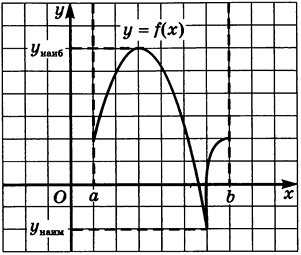
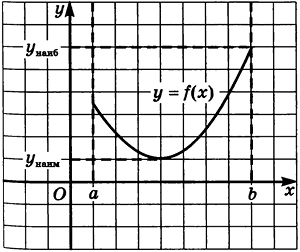
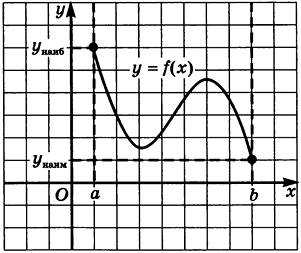
Пример 1: Графическое решение

Рассмотрим функцию y = \cfrac{x}{1 + x^2} . Построив её график (см. рисунок ), можно сделать вывод, что наибольшее значение функции достигается в точке x = 1 и равно y_{\text{макс}} = \cfrac{1}{2} , а наименьшее значение достигается в точке x = -1 и равно y_{\text{мин}} = -\cfrac{1}{2} .

Графический метод полезен для наглядной оценки, но он не всегда удобен, особенно при сложных функциях или когда точное значение экстремума требуется в аналитической форме. В таких случаях используется производная.

Теорема о наибольшем и наименьшем значении функции

Теорема гласит, что если функция f(x) непрерывна на отрезке [a; b] , то она обязательно достигает на этом отрезке своего наибольшего и наименьшего значений. Эти значения могут достигаться как на концах отрезка, так и внутри его.

Функции на различных интервалах могут вести себя по-разному. Рассмотрим несколько возможных случаев:

1. Наибольшее и наименьшее значения достигаются внутри отрезка .
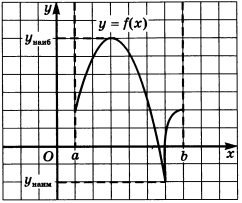2. Наибольшее значение достигается на конце отрезка, а наименьшее — внутри .
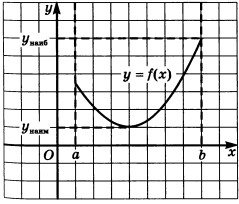3. Оба значения достигаются на концах отрезка

.

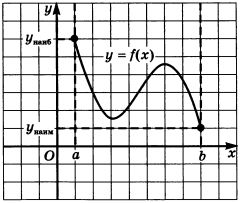Алгоритм нахождения наибольшего и наименьшего значений функции

Чтобы найти наибольшее и наименьшее значения непрерывной функции y = f(x) на отрезке [a; b] , следует воспользоваться следующим алгоритмом:

1. Найти производную f'(x) .
2. Найти стационарные и критические точки функции внутри отрезка [a; b] .
3. Вычислить значения функции f(x) в критических точках и на концах отрезка a и b .
4. Сравнить полученные значения и выбрать наибольшее и наименьшее.

Пример 1: Решение с использованием производной

Найдем наибольшее и наименьшее значения функции y = x^3 - 3x^2 - 45x + 1 на трёх различных интервалах.

а) На отрезке [-4; 6]

1. Производная функции:

   y' = 3x^2 - 6x - 45

2. Стационарные точки найдём из уравнения y' = 0 :

   3x^2 - 6x - 45 = 0 \quad \Rightarrow \quad x^2 - 2x - 15 = 0

   Решим квадратное уравнение:

   x_1 = -3, \quad x_2 = 5

3. Оба корня принадлежат заданному отрезку [-4; 6] , поэтому составим таблицу значений функции в точках x = -4 , x = -3 , x = 5 , x = 6 :

x	y
-4	69
-3	82
5	-174
6	-161

Наименьшее значение: y_{\text{мин}} = -174 при x = 5 , наибольшее значение: y_{\text{макс}} = 82 при x = -3 .

б) На отрезке [0; 6]

1. Производная та же: y' = 3x^2 - 6x - 45 .
2. Из стационарных точек только x = 5 принадлежит отрезку [0; 6] .
3. Составим таблицу значений функции в точках x = 0 , x = 5 , x = 6 :

x	y
0	1
5	-174
6	-161

Наименьшее значение: y_{\text{мин}} = -174 при x = 5 , наибольшее значение: y_{\text{макс}} = 1 при x = 0 .

в) На отрезке [-2; 2]

На этом отрезке нет стационарных точек, поэтому вычислим значения функции на концах отрезка:

x	y
-2	71
2	-93

Наименьшее значение: y_{\text{мин}} = -93 , наибольшее значение: y_{\text{макс}} = 71 .

Пример 2: Кусочная функция

Найдем наибольшее и наименьшее значения функции y = 5x^3 - x|x - 1| на отрезке [0; 2] .

1. Разобьём функцию на две части в зависимости от значения x :

   f(x) = \begin{cases} 5x^3 - x^2 + x, \text{если } x \geqslant 1 \\ 5x^3 + x^2 - x, \text{если } x \lt 1 \end{cases}

2. Производная для x \gt 1 : f'(x) = 15x^2 - 2x + 1 . Решения уравнения f'(x) = 0 нет.

   Производная для x \lt 1 : f'(x) = 15x^2 + 2x - 1 . Решив уравнение f'(x) = 0 , находим x = \cfrac{1}{5} .

3. Критические точки: x = 0 , x = 1 , x = 2 , x = \cfrac{1}{5} . Составим таблицу значений функции:

x	y
0	0
\cfrac{1}{5}	-\cfrac{3}{25}
1	5
2	38

Наименьшее значение: y_{\text{мин}} = -\cfrac{3}{25} , наибольшее значение: y_{\text{макс}} = 38 .

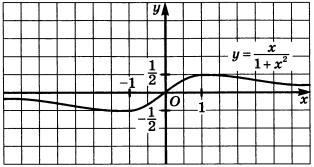
Пример 3: Функция на луче

Найдем наибольшее значение функции y = \cfrac{x}{1 + x^2} на луче [0; +\infty) .

1. Производная функции:

   y' = \cfrac{1 - x^2}{(1 + x^2)^2}

2. Решим уравнение y' = 0 : 1 - x^2 = 0 , откуда x = 1 .

3. Поскольку x = 1 — точка максимума, наибольшее значение функции:

   y_{\text{макс}} = \cfrac{1}{2}

Подберите подходящий график

• Наибольшее и наименьшее значения достигаются внутри отрезка.

• Наимень­шее значение достигается внутри отрезка, а наибольшее — в правом конце.

• На рисунке и наибольшее и наименьшее зна­чения достигаются на концах отрезка.

y=\cfrac{3}{x}, \quad[0,3 ; 2]

Производная функции:

y^{\prime}(x)=3\left(\frac{1}{x}\right)^{\prime}=3 \cdot\left(-\frac{1}{x^{2}}\right)=-\frac{3}{x^{2}}<0

Выражение имеет смысл при:

x \neq 0

Значения функции:

\begin{aligned} & y(0,3)=\frac{3}{0,3}=\frac{30}{3}=10 \\ & y(2)=\frac{3}{2}=1,5 \end{aligned}

Ответ: y_{\text {наим }}=1,5 ; y_{\text {наиб }}=10.

y=-\cfrac{8}{x},\left[\cfrac{1}{4} ; 8\right];

Производная функции:

y^{\prime}(x)=-8\left(\frac{1}{x}\right)^{\prime}=-8 \cdot\left(-\frac{1}{x^{2}}\right)=\frac{8}{x^{2}}>0

Выражение имеет смысл при:

x \neq 0

Значения функции:

\begin{aligned} & y\left(\frac{1}{4}\right)=-8 \cdot \frac{1}{4}=-8 \cdot 4=-32 ; \\ & y(8)=-\frac{8}{8}=-1 ; \end{aligned}

Ответ: y_{\text {наим }}=-32 ; y_{\text {наиб }}=-1.

y=3 x-6,[-1 ; 4];

Производная функции:

y^{\prime}(x)=(3 x-6)^{\prime}=3>0

Значения функции:

\begin{aligned} & y(-1)=3 \cdot(-1)-6=-3-6=-9 ; \\ & y(4)=3 \cdot 4-6=12-6=6 ; \\ & \text { Ответ: } y_{\text {наим }}=-9 ; y_{\text {наиб }}=6 . \end{aligned}

y=-2 \cos x,\left[-2 \pi ;-\cfrac{\pi}{2}\right];

Производная функции:

y^{\prime}(x)=-2(\cos x)^{\prime}=-2 \cdot(-\sin x)=2 \sin x

Стационарные точки:

\begin{aligned} & 2 \sin x=0 \\ & \sin x=0 \\ & x=\pi n \end{aligned}

Значения функции:

y(-2 \pi)=-2 \cos (-2 \pi)=-2 \cos 2 \pi=-2 \begin{aligned} & y(-\pi)=-2 \cos (-\pi)=-2 \cos \pi=2 \\ & y\left(-\frac{\pi}{2}\right)=-2 \cos \left(-\frac{\pi}{2}\right)=-2 \cos \frac{\pi}{2}=0 \end{aligned}

Ответ: y_{\text {наим }}=-2 ; y_{\text {наиб }}=2.

y=6 \cos x,\left[-\frac{\pi}{2} ; 0\right];

Производная функции:

y^{\prime}(x)=6(\cos x)^{\prime}=6 \cdot(-\sin x)=-6 \sin x

Стационарные точки:

\begin{aligned} & -6 \sin x=0 \\ & \sin x=0 \\ & x=\pi n \end{aligned}

Значения функции:

\begin{aligned} & y\left(-\frac{\pi}{2}\right)=6 \cos \left(-\frac{\pi}{2}\right)=6 \cos \frac{\pi}{2}=0 \\ & y(0)=6 \cos 0=6 \end{aligned}

Ответ: y_{\text {наим }}=0 ; y_{\text {наиб }}=6.

y=-0,5 \sin x,\left[-\frac{\pi}{2} ; \frac{\pi}{2}\right];

Производная функции:

y^{\prime}(x)=-0,5(\sin x)^{\prime}=-0,5 \cos x

Стационарные точки:

\begin{aligned} & -0,5 \cos x=0 \\ & \cos x=0 \\ & x=\frac{\pi}{2}+\pi n \end{aligned}

Значения функции:

\begin{aligned} & y\left(-\frac{\pi}{2}\right)=-0,5 \sin \left(-\frac{\pi}{2}\right)=0,5 \sin \frac{\pi}{2}=0,5 \\ & y\left(\frac{\pi}{2}\right)=-0,5 \sin \frac{\pi}{2}=-0,5 \end{aligned}

Ответ: y_{\text {наим }}=-0,5 ; y_{\text {наиб }}=0,5.

y=\operatorname{tg} x,\left[-\frac{\pi}{3} ;-\frac{\pi}{6}\right];

Производная функции:

y^{\prime}(x)=(\operatorname{tg} x)^{\prime}=\frac{1}{\cos ^2 x}>0

Выражение имеет смысл при:

x \neq \frac{\pi}{2}+\pi n

Значения функции:

\begin{aligned} & y\left(-\frac{\pi}{3}\right)=\operatorname{tg}\left(-\cfrac{\pi}{3}\right)=-\operatorname{tg} \cfrac{\pi}{3}=-\sqrt{3} ; \\ & y\left(-\frac{\pi}{6}\right)=\operatorname{tg}\left(-\cfrac{\pi}{6}\right)=-\operatorname{tg} \cfrac{\pi}{6}=-\cfrac{\sqrt{3}}{3} \\ & \text { Ответ: } y_{\text {наим }}=-\sqrt{3} ; y_{\text {наиб }}=-\cfrac{\sqrt{3}}{3} . \end{aligned}

y=\cfrac{1}{2} \operatorname{tg} x, \quad\left[-\pi ;-\cfrac{3 \pi}{4}\right];

Производная функции:

y^{\prime}(x)=\frac{1}{2}(\operatorname{tg} x)^{\prime}=\frac{1}{2} \cdot \frac{1}{\cos ^2 x}>0

Выражение имеет смысл при:

x \neq \frac{\pi}{2}+\pi n

Значения функции:

\begin{aligned} & y(-\pi)=\frac{1}{2} \operatorname{tg}(-\pi)=-\frac{1}{2} \operatorname{tg} \pi=0 \\ & y\left(-\frac{3 \pi}{4}\right)=\frac{1}{2} \operatorname{tg}\left(-\frac{3 \pi}{4}\right)=\frac{1}{2} \operatorname{tg}\left(-\pi+\frac{\pi}{4}\right)=\frac{1}{2} \operatorname{tg} \frac{\pi}{4}=\frac{1}{2} \end{aligned}

Ответ: y_{\text {наим }}=0 ; y_{\text {наиб }}=0,5.

y=-3 \operatorname{tg} x,\left[\pi ; \frac{4 \pi}{3}\right];

Производная функции:

y^{\prime}(x)=-3(\operatorname{tg} x)^{\prime}=-3 \cdot \frac{1}{\cos ^2 x}<0

Выражение имеет смысл при:

x \neq \frac{\pi}{2}+\pi n

Значения функции:

\begin{aligned} & y(\pi)=-3 \operatorname{tg} \pi=0 \\ & y\left(\frac{4 \pi}{3}\right)=-3 \operatorname{tg} \cfrac{4 \pi}{3}=-3 \operatorname{tg} (\cfrac{\pi}{3}+\pi)=-3 \sqrt{3} ; \\ & \text { Ответ: } y_{\text {наим }}=-3 \sqrt{3} ; y_{\text {наиб }}=0 . \end{aligned}

y=-2 \operatorname{tg} x, \quad\left[0 ; \frac{\pi}{6}\right];

Производная функции:

y^{\prime}(x)=-2(\operatorname{tg} x)^{\prime}=-2 \cdot \frac{1}{\cos ^2 x}<0

Выражение имеет смысл при:

x \neq \frac{\pi}{2}+\pi n

Значения функции:

\begin{aligned} & y(0)=-2 \operatorname{tg} 0=0 \\ & y\left(\frac{\pi}{6}\right)=-2 \operatorname{tg} \frac{\pi}{6}=-2\frac{ \sqrt{3}}{3} \end{aligned}

Ответ: y_{\text {наим }}=-\frac{2 \sqrt{3}}{3} ; y_{\text {наиб }}=0.