Тест по теме: Ускорение

Как изменяются данные спидометра при начале движения автомобиля и его торможении? Какая физическая характеристика отвечает за изменение скорости?

Попробуйте бросить мяч вверх и проанализируйте, как изменяется его скорость в процессе движения.

Когда тела находятся в движении, их скорость может изменяться в нескольких аспектах: увеличиваться или уменьшаться (по модулю), менять направление либо подвергаться изменениям сразу и в модуле, и в направлении.

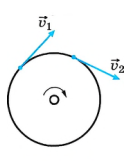
Примером может служить шайба, скользящая по льду, скорость которой со временем уменьшается, пока она полностью не остановится. Если держать камень в руках и отпустить его, скорость падающего камня начнёт постепенно увеличиваться. При постоянной скорости вращения точильного круга скорость любой его точки остаётся неизменной по величине, но изменяется в направлении

Если же бросить камень под углом к горизонту, его скорость будет изменяться одновременно и по величине, и по направлению.

Изменение скорости может происходить за разное время: от крайне быстрого (например, движение пули в стволе винтовки) до относительно медленного (разгон поезда при отправлении).

---

Важно знать: физическая величина, характеризующая скорость изменения движения, называется ускорением.

---

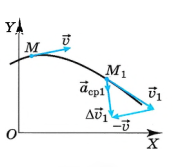
Для иллюстрации рассмотрим криволинейное и неравномерное движение. В такой ситуации скорость точки меняется и по величине, и по направлению. Пусть в определённый момент времени t точка находится в положении M и обладает скоростью \vec{v}.

Через интервал времени \Delta t_1 точка оказывается в новом положении M_1 с другой скоростью \overrightarrow{v_1}. Тогда изменение скорости за промежуток \Delta t_1 будет равно:

\Delta \overrightarrow{v_1} = \overrightarrow{v_1} - \vec{v}.

Вычитание вектора \vec{v} выполняется путём прибавления к \overrightarrow{v_1} противоположного вектора (-\vec{v}) :

\Delta \overrightarrow{v_1} = \overrightarrow{v_1} - \vec{v} = \overrightarrow{v_1} + (-\vec{v}).

По правилу сложения векторов вектор изменения скорости \Delta \overrightarrow{v_1} направлен из начала вектора \overrightarrow{v_1} в конец вектора -\vec{v} , как показано на рисунке

Практическое задание:

Понаблюдайте за тем, как начинает движение любое тело. Что можно сказать о его скорости? Приведите примеры движения, где скорость изменяется только в направлении или только в модуле.

---

Разделив вектор \Delta \overrightarrow{v_1} на временной интервал \Delta t_1, получим новый вектор, направленный так же, как \Delta \overrightarrow{v_1}. Этот вектор называется средним ускорением за промежуток времени \Delta t_1. Обозначим его как \vec{a}_{\text{ср}1}:

\vec{a}_{\text{ср}1} = \frac{\Delta \overrightarrow{v_1}}{\Delta t}.

---

Мгновенное ускорение

По аналогии с определением мгновенной скорости вводится понятие мгновенного ускорения. Рассмотрим последовательность средних ускорений для всё меньших интервалов времени:

\vec{a}_{\text{ср}2} = \frac{\Delta \overrightarrow{v_2}}{\Delta t}, \ldots

При уменьшении \Delta t вектор \Delta \vec{v} становится всё меньше по модулю и изменяется по направлению .

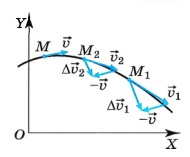
Средние ускорения также изменяются, но при стремлении \Delta t \to 0 отношение \Delta \vec{v} / \Delta t становится всё ближе к определённому значению. Это значение в механике называют ускорением точки в данный момент времени, или просто ускорением, обозначая как \vec{a}.

---

Определение: ускорение — это предел отношения изменения скорости \Delta \vec{v} к интервалу времени \Delta t, за который произошло это изменение, при \Delta t \to 0.

---

Ускорение имеет то же направление, что и вектор \Delta \vec{v} при \Delta t \to 0. Но в отличие от скорости, его направление нельзя определить, просто зная траекторию движения и направление точки по ней. На примерах в дальнейшем мы разберём способы определения направления ускорения.

---

Общий случай:

Ускорение направлено под углом к вектору скорости.

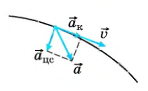
Полное ускорение, описывающее изменение скорости по величине и направлению, часто разлагают на две составляющие:

1. Касательное ускорение (\vec{a}_k) характеризует изменение скорости по модулю и направлено по касательной к траектории.
2. Центростремительное ускорение (\vec{a}_z) описывает изменение направления скорости и всегда направлено к центру кривизны траектории.

Рассмотрим два особых случая:

1. При движении точки по прямой её скорость изменяется только по модулю.
2. Если точка равномерно движется по окружности, её скорость меняется только в направлении.

---

Единицы измерения ускорения

Движение точки может быть как с постоянным ускорением, так и с переменным. Если ускорение неизменно, то отношение изменения скорости к времени остаётся одинаковым для любого временного интервала. Тогда:

\vec{a} = \frac{\Delta \vec{v}}{\Delta t}.

Положительное значение времени (\Delta t > 0) указывает, что при постоянном ускорении вектор ускорения направлен так же, как вектор изменения скорости.

---

Формула модуля ускорения:

|\vec{a}| = \frac{|\Delta \vec{v}|}{\Delta t}.

---

Единица измерения ускорения: если скорость измеряется в метрах в секунду (\text{м/с}), а время — в секундах, то ускорение выражается в \text{м/с}^2. Это значит, что модуль ускорения равен единице, если за 1 секунду модуль скорости изменяется на 1 м/с.