Тест по теме: Уравнение прямолинейного равномерного движения

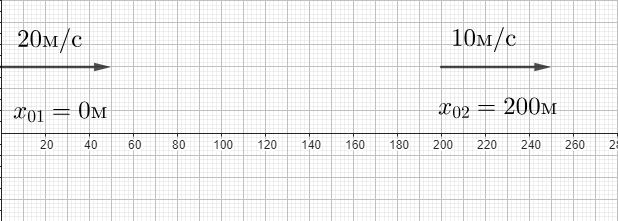
Тело может преодолевать одинаковый путь за разное время. Для описания быстроты движения введена физическая величина – скорость. Зная её, можно определить положение тела в любой момент времени.

Определение равномерного движения

Равномерным называется движение точки, при котором за любые равные промежутки времени точка проходит одинаковые пути. Оно может быть прямолинейным или криволинейным. Мы начнём с изучения равномерного прямолинейного движения, как наиболее простого вида.

Скорость

Скорость – величина, характеризующая движение. Например, черепаха движется медленно, человек – быстрее, автомобиль – ещё быстрее, а самая высокая скорость достигается с помощью космических ракет.

В механике скорость рассматривается как векторная величина, то есть она имеет модуль и направление.

Определение скорости:

Пусть точка движется равномерно прямолинейно. За время \Delta t она перемещается из точки M_1 в точку M_2, совершая перемещение \Delta \vec{r}. Тогда скорость \vec{v} равна отношению вектора перемещения к интервалу времени:

\vec{v} = \frac{\Delta \vec{r}}{\Delta t}.

Поскольку время \Delta t > 0, направление скорости совпадает с направлением перемещения \Delta \vec{r}.

Модуль скорости:

Модуль скорости v рассчитывается по формуле:

v = \frac{|\Delta \vec{r}|}{\Delta t}.

Здесь |\Delta \vec{r}| – расстояние, пройденное точкой за время \Delta t. Так как движение равномерное, v численно равно пути, который точка проходит за единицу времени.

Уравнение равномерного прямолинейного движения

Для описания движения точки в любой момент времени используется уравнение. Пусть начальное положение точки задаётся радиус-вектором \vec{r}_0, а вектор \vec{r} указывает её положение через время t. Тогда:

\vec{v} = \frac{\vec{r} - \vec{r}_0}{t}.

При t_0 = 0, уравнение скорости записывается так:

\vec{r} = \vec{r}_0 + \vec{v}t.

В декартовой системе координат:

Если точка движется вдоль оси OX, уравнение в проекциях на оси будет:

x = x_0 + v_x t, \quad y = y_0, \quad z = z_0.

Для одномерного случая путь s определяется как модуль изменения координаты:

s = |x_2 - x_1| = v t.

Если движение направлено против оси OX, используется уравнение:

x = x_0 \pm v t.

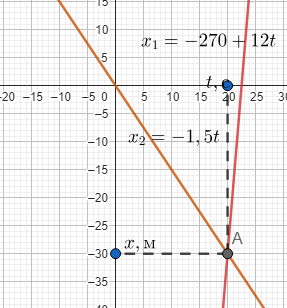
Графическое представление

На графике зависимость проекции скорости от времени v_x(t) для равномерного движения представлена прямой, параллельной оси времени. Площадь под графиком равна изменению координаты:

\Delta x = v_x t.

На графике зависимости координаты от времени x(t) равномерное движение отображается прямой линией. Угол наклона линии к оси времени зависит от величины скорости. Чем больше скорость, тем круче наклон.

Приближённость реального движения

Абсолютно равномерное прямолинейное движение не существует: автомобиль на шоссе слегка отклоняется от прямой и изменяет скорость. Но для коротких интервалов времени такое движение можно считать равномерным и прямолинейным с достаточной точностью.

Вывод:
Равномерное прямолинейное движение – это основа кинематики. Уравнение движения позволяет рассчитывать положение точки в любой момент времени, а графики помогают наглядно анализировать движение.

\vec{r}=\vec{r_0}+\vec{v}t

Выведите уравнение движение из формулы скорости

\vec{v}=\cfrac{\Delta \vec{r}}{\Delta t}= \cfrac{ \vec{r} -\vec{r}_0 }{ t-t_0}= \cfrac{ \vec{r} -\vec{r}_0 }{ t}

\vec{r}=\vec{r}_0+\vec{v}t

В проекциях на ось ОХ уравнение движения можно записать в виде

x=x_0+v_xt

Движение грузового автомобиля описывается уравнением x_1=-270+12 t , а движение пешехода по обочине того же шоссе - уравнением x_2=-1,5 t . С какими скоростями и в каком направлении они двигались? Когда и где они встретились?
Для того, чтобы найти время их встречи, приравниваем правые части уравнений движения:

-270+12 t=-1,5 t

13,5 t=270 ;

t=\cfrac{270}{13,5}=20 \mathrm{c} \text {; }

Подставим время в уравнение движения:

x=-1,5 \cdot t=-1,5 \cdot 20=-30 \mathrm{~m}

По прямому шоссе в одном направлении движутся два мотоциклиста. Скорость первого мотоциклиста 10 \mathrm{~m} / \mathrm{c} . Второй догоняет его со скоростью 20 \mathrm{~m} / \mathrm{c} . Расстояние между мотоциклистами в начальный момент времени равно 200 м. Найти время и место встречи мотоциклистов.

1. Примем за начало координат место нахождения второго мотоциклиста, тогда:
   x_{01}=200 \mathrm{~m} ; x_{02}=0 ;

2. Напишем уравнение движения мотоциклистов:
   x_{1}=200+10 t ; x_{2}=20 t ;

3. Найдем время встречи приравнивая правые части уравнений движения:
   20 t=200+10 t ,
   отсюда 10 t=200 ,
   значит t=20 \mathrm{c} ;

4. Найдем место встречи, подставив время в уравнение:
   x=20 \cdot 20=400 \mathrm{~m} ;