Тест по теме: Сложение скоростей

Сложение скоростей

Введение

Когда мы описываем движение, важно учитывать, в какой системе координат это происходит. Например:

• Если моторная лодка плывёт по реке, её скорость относительно воды будет отличаться от скорости относительно берега, так как река течёт.

Чтобы связать эти скорости, используют закон сложения скоростей. Этот закон описывает, как движение тела в одной системе координат преобразуется при переходе в другую.

---

Основные понятия

1. Скорость лодки относительно воды

Обозначим скорость лодки относительно воды как \vec{v}_1. Вода сама может двигаться относительно берега со скоростью течения \vec{v}.

2. Скорость лодки относительно берега

Скорость лодки относительно берега обозначим \vec{v}_2. Чтобы найти её, нужно сложить две скорости:
\vec{v}_2 = \vec{v}_1 + \vec{v}.

Здесь складываются векторы, поэтому учтите их направления.

---

Обоснование закона сложения скоростей

Рассмотрим движение лодки в двух системах координат:

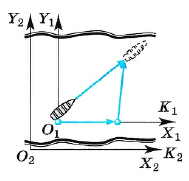
• Система K_1: движется вместе с водой. В этой системе координат лодка имеет перемещение \Delta \vec{r}_1.
• Система K_2: неподвижна относительно берега. В этой системе лодка имеет перемещение \Delta \vec{r}_2, а вода — \Delta \vec{r}.

В течение времени \Delta t выполняется:
\Delta \vec{r}_2 = \Delta \vec{r}_1 + \Delta \vec{r}.

Разделим обе стороны на \Delta t:
\frac{\Delta \vec{r}_2}{\Delta t} = \frac{\Delta \vec{r}_1}{\Delta t} + \frac{\Delta \vec{r}}{\Delta t}.

Так как отношение перемещения ко времени — это скорость, то:
\vec{v}_2 = \vec{v}_1 + \vec{v}.

---

Скалярные компоненты скоростей

Если движение происходит в плоскости, каждая скорость имеет проекции на оси координат:
\begin{aligned} v_{2x} &= v_{1x} + v_x, \\ v_{2y} &= v_{1y} + v_y. \end{aligned}

Это уравнения для сложения проекций скоростей по осям x и y.

---

Графическая интерпретация

Сложение скоростей можно изобразить геометрически:

1. Постройте вектор \vec{v}_1 на плоскости.
2. От его конца отложите вектор \vec{v}.
3. Вектор, соединяющий начало \vec{v}_1 с концом \vec{v}, — это \vec{v}_2.

Такой подход наглядно демонстрирует, как складываются скорости.

---

Пример

Условие:
Лодка движется со скоростью \vec{v}_1 = 4 \, \text{м/с} относительно воды. Скорость течения \vec{v} = 3 \, \text{м/с}, направленная под углом 60^\circ к направлению движения лодки. Найдите скорость лодки относительно берега.

Решение:
Используем закон сложения скоростей:
\vec{v}_2 = \vec{v}_1 + \vec{v}.

Воспользуемся компонентами скоростей:
v_{2x} = v_{1x} + v_x = 4 + 3 \cdot \cos 60^\circ = 4 + 1.5 = 5.5 \, \text{м/с},
v_{2y} = v_{1y} + v_y = 0 + 3 \cdot \sin 60^\circ = 0 + 2.6 \, \text{м/с}.

Найдем модуль результирующей скорости:
v_2 = \sqrt{v_{2x}^2 + v_{2y}^2} = \sqrt{5.5^2 + 2.6^2} \approx 6.1 \, \text{м/с}.

---

Итоги

1. Закон сложения скоростей:
   \vec{v}_2 = \vec{v}_1 + \vec{v}.
2. Скорости складываются как векторы, учитывая их модули и направления.
3. В каждой задаче важно правильно выбрать систему координат и определить проекции скоростей.

Вывод: Закон сложения скоростей помогает связывать движения в разных системах координат, что важно в задачах кинематики. {card}!