Тест по теме: Движение с ускорением свободного падения

ДВИЖЕНИЕ С ПОСТОЯННЫМ УСКОРЕНИЕМ СВОБОДНОГО ПАДЕНИЯ

Свободное падение тел изучается в предположении, что ускорение свободного падения остается неизменным, а сопротивление воздуха не учитывается.

Такое движение описывается кинематическими уравнениями (1.13) и (1.15), которые были ранее выведены.

Движение с постоянным ускорением может быть как прямолинейным, так и криволинейным. Если начальная скорость точки равна нулю или совпадает по направлению с вектором ускорения, то движение будет прямолинейным вдоль этой линии. В случае, когда направления начальной скорости и ускорения различны, траектория точки становится криволинейной.

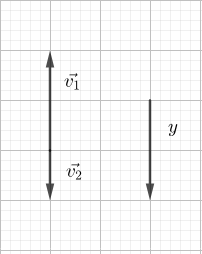
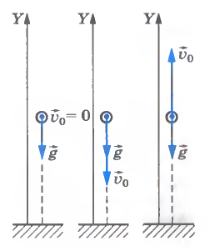
Ускорение свободного падения всегда направлено вертикально вниз. Таким образом, тело движется прямолинейно, если его начальная скорость равна нулю или направлена вдоль вертикали (рис.). Если же начальная скорость тела имеет наклон к вертикали, траектория становится криволинейной.

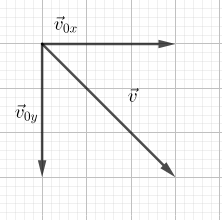
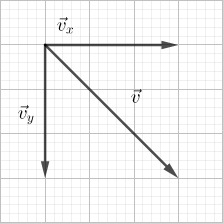
Часто в задачах встречаются примеры движения тел, которым придана начальная скорость под углом к горизонту. Например, это может быть снаряд, выстреленный из пушки, или ядро, толкнутое спортсменом.

Определим траекторию тела, брошенного под углом к горизонту, предполагая, что ускорение свободного падения остаётся постоянным на всём пути. Пусть тело брошено из точки O с начальной скоростью \vec{v}_0 под углом \alpha к горизонту

. Для анализа выберем систему координат так, чтобы векторы \vec{v}_0 и \vec{g} находились в одной плоскости, например, в XOY. Направим ось OX горизонтально, а ось OY — вертикально вверх. Начало координат будет в точке броска.

Так как ускорение свободного падения неизменно, движение тела можно описать уравнениями:

x = x_0 + v_{0x} t + \cfrac{a_x t^2}{2}

y = y_0 + v_{0y} t + \cfrac{a_y t^2}{2}.

В заданной системе координат x_0 = 0 и y_0 = 0. Проекции вектора на оси можно выразить через модуль вектора и тригонометрические функции угла между вектором и положительным направлением оси. На основании рисунка 1.35:

v_{0x} = v_0 \cos \alpha, \quad v_{0y} = v_0 \sin \alpha, \quad a_x = 0, \quad a_y = -g.

Подставляя эти значения в уравнения (1.17) и (1.18), получаем:

\begin{aligned} & x = v_0 \cos \alpha \cdot t, \\ & y = v_0 \sin \alpha \cdot t - \frac{g t^2}{2}. \end{aligned}

Для построения траектории можно вычислить значения координат x и y в различные моменты времени, а затем соединить полученные точки плавной линией. Однако более удобно вывести уравнение траектории, то есть зависимость y от x.

Из уравнения (1.19) выразим t:

t = \frac{x}{v_0 \cos \alpha}.

Подставляя это значение в уравнение (1.20), находим:

y = x \frac{v_0 \sin \alpha}{v_0 \cos \alpha} - \frac{g x^2}{2 v_0^2 \cos^2 \alpha}.

Преобразуем:

y = x \tan \alpha - \frac{g}{2 v_0^2 \cos^2 \alpha} x^2.

Обозначим: \tan \alpha = c, \quad -\frac{g}{2 v_0^2 \cos^2 \alpha} = b. Тогда уравнение принимает вид:

y = b x^2 + c x.

График функции (1.21) представляет собой параболу с осью симметрии, параллельной оси Y. Поскольку b < 0, ветви параболы направлены вниз. На рисунке 1.36 показан пример такой параболы, где b = -0.2 \, \text{м}^{-1} и c = 1.6. Таким образом, доказано, что при постоянном ускорении свободного падения траектория тела, брошенного под углом к горизонту, является параболой.

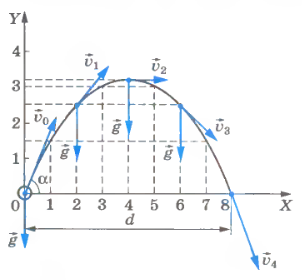
Теперь рассмотрим случай, когда начальная скорость тела направлена горизонтально. Из рисунка видно, что с момента, когда скорость становится горизонтальной, тело движется по ветви параболы. Следовательно, любое тело, брошенное горизонтально, будет двигаться по одной из ветвей параболы, вершина которой совпадает с точкой бросания

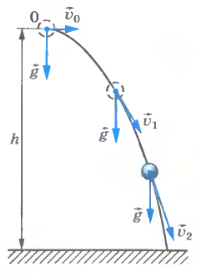
Наглядное представление траектории тела, брошенного горизонтально или под углом к горизонту, можно получить наглядно, используя простой опыт (рис. 1.38). Каждая частица воды в струе движется по параболе, поэтому струя воды принимает параболическую форму. Это можно легко проверить, установив за струёй экран с заранее нарисованной параболой. Если подобрать скорость истечения воды, струя будет совпадать с нарисованной параболой.

v_{0x}= v_{0} \cos\alpha

v_{0y}= v_{0} \sin\alpha -gt

Напишите формулы координат учитывая что x_0=0, y_0=0

x= v_0 \cos\alpha t

y= v_0 \sin\alpha t -\cfrac{ g t^2 }{2}

Тело будет лететь пока высота не станет равной 0 , соответственно чтобы найти время, приравняем формулу координаты y к нуль и решим уравнения относительно времени v_0\sin\alpha t-\cfrac{gt^2}{2} =0

v_0\sin\alpha t= \cfrac{gt^2}{2}

v_0\sin\alpha= \cfrac{gt}{2}

t=\cfrac{2 v_0 \sin\alpha }{ g }

Зная время полета можно найти расстояние учитывая что t=\cfrac{ 2 v_0 \sin\alpha }{ g }

l=v_{0x}t= v_0\cos \alpha \cdot \cfrac{2 v_0\sin\alpha }{g}=

\cfrac{ v^2_0 \sin2\alpha }{g}

С высокого отвесного обрыва начинает свободно падать камень. Какую скорость он будет иметь через 5 с после начала падения?

t=5 с

v=v_0+gt

v=10 \cdot 5=50 м/с

Камень брошен вертикально вверх с начальной скоростью 20 м/с. Чему будет равен модуль скорости камня через 1,5 с после начала движения? v_0 = 20 м/с t=1,5 с

v=v_0-g t=20-1,5 \cdot 10=5 м / с

Тело свободно падает из состояния покоя. Определите, на сколько увеличивается скорость тела за третью секунду падения.

v_3=v(3)-v(2)

За 3 секунду

v_{(3)}=v_0+g t_3

t_3=3 c

v_3=10 \cdot 3=30 м/с

За 2 секунду

v_{(2)}=v_0+g t_2

t_2=2 c

v_2=10 \cdot 2=20 м/с

v_3=30-20=10 м/с

Камень брошен с некоторой высоты вертикально вниз с начальной скоростью 2 м/с. Чему будет равна скорость камня через 0,6 с после броска?

v_0=2м/с

t=0.6 с

v=v_0+g t

v=2+ 10 \cdot 0,6=8 м /с

Тело брошено вертикально вверх со скоростью 30 м/с. Через какое время скорость этого тела изменит направление на противоположное и станет равной 10 м/с ?

v_1=30 м/с

v_2=10 м/с

\vec{v_2}=\vec{v_1}+\vec{g} t

Oy: v_2=-v_1+g t

t=\cfrac{v_2+v_1}{g}=\cfrac{40}{10}=4 \mathrm{с}

С высоты 12 м над землёй без начальной скорости падает тело. На какой высоте окажется тело через 1 с после начала падения?

h=12 м-общая высота

t_1=1с

За 1 ю секунду

h_0=\cfrac{g t_1^2}{2}=\cfrac{10 \cdot 1}{2}=5м

h_1=h-h_0=12-5=7м

Тело брошено вертикально вверх с высоты 40 м с начальной скоростью 5 м/с. На какой высоте окажется тело через 2 с?

h_0 = 40 м

v_0 = 5 м/c

t = 2 c

h=h_0+v_0 t-\cfrac{g t^2}{2}=

40+5 \cdot 2-\cfrac{10 \cdot 4}{2}=30 м

Мяч, брошенный вертикально вверх, упал на землю через 3 с. Определите начальную скорость.

t=3c

v_0 t-\cfrac{g t^2}{2}=0

v_0=\cfrac{g t}{2}=\cfrac{10\cdot3}{2}=15 м/с

С башни высотой 45 м горизонтально брошен камень. Через какое время он упадёт на землю?

h_0 =45 м

h=h_0-\cfrac{g t^2}{2}=0

h_0=\cfrac{g t^2}{2} \Rightarrow

t=\sqrt{\cfrac{2 h}{g}}=\sqrt{\cfrac{2 90}{10}}=3 c

Тело бросили горизонтально с начальной скоростью 40 м/с. Определите его скорость через 3 с.

v_{0 x}=40 м/ с

t=3с

v_{0 y}=g t=10 \cdot 3=30 м/ с

\vec{v}=\vec{v}{0 x}+\vec{v}{0 y}

v=\sqrt{v_{0x}^2+v_{0y}^2}=\sqrt{40^2+30^2}=50м/с

Камень, брошенный горизонтально со скоростью 15 м/с, упал на землю со скоростью 25 м/с. Сколько времени длился полёт камня?

v_x=15 м/с

v=25 м/с

\vec{v}=\vec{v}_x+\vec{v}_y

v_y^2+v_x^2=v^2 \Rightarrow v_y=\sqrt{v^2-v_x^2}

=\sqrt{625-225}=20 м /с

v_y=g t

t=\cfrac{v_y}{g}=\cfrac{20}{10}=2 c

Тело брошено горизонтально со скоростью 15 м/с. Через какое время от начала движения горизонтальное смещение будет равно вертикальному?

v_x=15 м /с

S_x=v_x t

S_y=\cfrac{g t^2}{2}

S_x=S_y

v_x t=\cfrac{g t^2}{2} \Rightarrow

t=\cfrac{2 v_x}{g}=\cfrac{2 \cdot 15}{10}=3 c

В начальный момент времени скорость тела направлена горизонтально и равна 15 м /с. Определите горизонтальное смещение тела к тому моменту времени, когда вертикальное перемещение будет равно 20 м.

v_x=15 \mathrm{~m} / \mathrm{c}

S_y=20 \mathrm{~m}

S_x=v_x t

S_y=\cfrac{g t^2}{2} \Rightarrow t=\sqrt{\cfrac{2 S_y}{g}}

S_x=v_x \cdot \sqrt{\cfrac{2 S_y}{g}}=15 \cdot \sqrt{\cfrac{2 \cdot 20}{10}}=30 м